
Glowworms above the Waitomo Stream, Waitomo Glowworm Cave, New Zealand (Image)
Previously Pre-Posted…
• Glow with the Flow #1


Glowworms above the Waitomo Stream, Waitomo Glowworm Cave, New Zealand (Image)
Previously Pre-Posted…
• Glow with the Flow #1
This is 2026. Headlines like this are NOT acceptable:
As soon as I saw that, I thought: “Harmful”? Harmful schmarmful! It should be toxic…
Funnily enough, when I looked at the story itself, it was toxic. That is, it was “toxic”:
That’s the way it should be. Or rather, the way it should be when English isn’t used the way it should be. As I’ve said pre-previously:
There’s only one word for it: toxic. The proliferation of this word is an incendiarily irritating abjectional aspect of contemporary culture. My visit to Google Ngram has confirmed my worst suspicions:
• Continue reading Get Your Tox Off
Here’s a second serendipitous fractal:
A serendipitous fractal on a fract-L
It looks like (and is related to) the limestone fractal and I found it similarly serendipitously. This time I was looking at continued fractions, a simple yet subtle and seductive way of representing non-integer numbers like 2/3 and 7/9 (or √2 and π). To generate a continued fraction from a/b < 1, you divide a/b into 1 and take away the integer part. Then you repeat with the remainder until nothing is left (or, as with irrationals like 1/√2 and 1/π, you've calculated long enough for your needs). The integers at each stage are the numbers of the continued fraction. Here is the working for contfrac(2/3), the continued fraction of 2/3:
int(1/(2/3)) = int(3/2) = int(1.5) = 1
3/2 – 1 = 1/2
int(1/(1/2)) = int(2) = 2
2 – 2 = 0contfrac(2/3) = 1, 2
By working backwards with (1, 2), you can use the continued fraction to reconstruct the original number a/b. Start with a/b = 0/1:
1 / (0/1 + 2) = 1 / ((0+2*1)/2) = 1 / (2/1) = 1/2
1 / (1/2 + 1) = 1 / ((1+2*1)/2) = 1 / (3/2) = 2/3
And here’s the working for contfrac(7/9), the continued fraction of 7/9:
int(1/(7/9)) = int(9/7) = int(1.285714…) = 1
9/7 – 1 = 2/7
int(1/(2/7)) = int(7/2) = int(3.5) = 3
7/2 – 3 = 1/2
int(1/(1/2)) = int(2) = 2
2 – 2 = 0contfrac(7/9) = 1, 3, 2
And here’s the reconstruction of 7/9 from its continued fraction, starting again with a/b = 0/1:
1 / (0/1 + 2) = 1 / ((0+2*1)/2) = 1 / (2/1) = 1/2
1 / (1/2 + 3) = 1 / ((1+2*3)/2) = 1 / (7/2) = 2/7
1 / (2/7 + 1) = 1 / ((2+7*1)/7) = 1 / (9/7) = 7/9
From that simple algorithm arise subtle and seductive things. Look at some continued fractions, cf(a/b), for a/b in simplest form (giving only the first few reciprocals, 1/b, because cf(1/b) = b). Interesting patterns appear, e.g. when a/b uses adjacent or nearly adjacent Fibonacci numbers:
cf(1/3) = 3 = cf(0.333333333…)
cf(2/3) = 1,2 = cf(0.666666666…)
cf(1/4) = 4 = cf(0.25)
cf(3/4) = 1,3 = cf(0.75)
cf(1/5) = 5 = cf(0.2)
cf(2/5) = 2,2 = cf(0.4)
cf(3/5) = 1,1,2 = cf(0.6)
cf(4/5) = 1,4 = cf(0.8)
cf(5/6) = 1,5 = cf(0.833333333…)
cf(2/7) = 3,2 = cf(0.285714285…)
cf(3/7) = 2,3 = cf(0.428571428…)
cf(4/7) = 1,1,3 = cf(0.571428571…)
cf(5/7) = 1,2,2 = cf(0.714285714…)
cf(6/7) = 1,6 = cf(0.857142857…)
cf(3/8) = 2,1,2 = cf(0.375)
cf(5/8) = 1,1,1,2 = cf(0.625)
cf(7/8) = 1,7 = cf(0.875)
cf(2/9) = 4,2 = cf(0.222222222…)
cf(4/9) = 2,4 = cf(0.444444444…)
cf(5/9) = 1,1,4 = cf(0.555555555…)
cf(7/9) = 1,3,2 = cf(0.777777777…)
cf(8/9) = 1,8 = cf(0.888888888…)
cf(3/10) = 3,3 = cf(0.3)
cf(7/10) = 1,2,3 = cf(0.7)
cf(9/10) = 1,9 = cf(0.9)
cf(2/11) = 5,2 = cf(0.181818181…)
cf(3/11) = 3,1,2 = cf(0.272727272…)
cf(4/11) = 2,1,3 = cf(0.363636363…)
cf(5/11) = 2,5 = cf(0.454545454…)
cf(6/11) = 1,1,5 = cf(0.545454545…)
cf(7/11) = 1,1,1,3 = cf(0.636363636…)
cf(8/11) = 1,2,1,2 = cf(0.727272727…)
cf(9/11) = 1,4,2 = cf(0.818181818…)
cf(10/11) = 1,10 = cf(0.909090909…)
cf(5/12) = 2,2,2 = cf(0.416666666…)
cf(7/12) = 1,1,2,2 = cf(0.583333333…)
cf(11/12) = 1,11 = cf(0.916666666…)
cf(2/13) = 6,2 = cf(0.153846153…)
cf(3/13) = 4,3 = cf(0.230769230…)
cf(4/13) = 3,4 = cf(0.307692307…)
cf(5/13) = 2,1,1,2 = cf(0.384615384…)
cf(6/13) = 2,6 = cf(0.461538461…)
cf(7/13) = 1,1,6 = cf(0.538461538…)
cf(8/13) = 1,1,1,1,2 = cf(0.615384615…)
cf(9/13) = 1,2,4 = cf(0.692307692…)
cf(10/13) = 1,3,3 = cf(0.769230769…)
cf(11/13) = 1,5,2 = cf(0.846153846…)
cf(12/13) = 1,12 = cf(0.923076923…)
cf(3/14) = 4,1,2 = cf(0.214285714…)
cf(5/14) = 2,1,4 = cf(0.357142857…)
cf(9/14) = 1,1,1,4 = cf(0.642857142…)
cf(11/14) = 1,3,1,2 = cf(0.785714285…)
cf(13/14) = 1,13 = cf(0.928571428…)
cf(2/15) = 7,2 = cf(0.133333333…)
cf(4/15) = 3,1,3 = cf(0.266666666…)
cf(7/15) = 2,7 = cf(0.466666666…)
cf(8/15) = 1,1,7 = cf(0.533333333…)
cf(11/15) = 1,2,1,3 = cf(0.733333333…)
cf(13/15) = 1,6,2 = cf(0.866666666…)
cf(14/15) = 1,14 = cf(0.933333333…)
cf(3/16) = 5,3 = cf(0.1875)
cf(5/16) = 3,5 = cf(0.3125)
cf(7/16) = 2,3,2 = cf(0.4375)
After investigating some of those patterns, I wondered what happened when you reversed the continued fraction cf(a/b) and used those reversed numbers backward (that is, used the numbers of cf(a/b) forward) to generate another and different a/b. And a/b will always be different unless cf(a/b) is a palindrome, like cf(5/12) = 2,2,2 or cf(5/13) = 2,1,1,2 or cf(4/15) = 3,1,3. Note that a continued fraction never ends in 1, so that when reversing, say, cf(5/8) = (1, 1, 1, 2), you need an adjustment from (2, 1, 1, 1) to (2, 1, 1+1) = (2, 1, 2). Here’s a little of what happens when you reverse cf(a1/b1) to generate a2/b2:
cf(1/2) = 2 → 2 = cf(1/2)
1/2 = 0.5 : 0.5 = 1/2
cf(1/3) = 3 → 3 = cf(1/3)
1/3 = 0.333333333 : 0.333333333 = 1/3
cf(2/3) = 1, 2 → 2, 1 → 3 = cf(1/3)
2/3 = 0.666666666 : 0.333333333 = 1/3
cf(3/4) = 1, 3 → 3, 1 → 4 = cf(1/4)
3/4 = 0.75 : 0.25 = 1/4
cf(2/5) = 2, 2 → 2, 2 = cf(2/5)
2/5 = 0.4 : 0.4 = 2/5
cf(3/5) = 1, 1, 2 → 2, 1, 1 → 2, 2 = cf(2/5)
3/5 = 0.6 : 0.4 = 2/5
cf(4/5) = 1, 4 → 4, 1 → 5 = cf(1/5)
4/5 = 0.8 : 0.2 = 1/5
cf(5/6) = 1, 5 → 5, 1 → 6 = cf(1/6)
5/6 = 0.833333333 : 0.166666666 = 1/6
cf(2/7) = 3, 2 → 2, 3 = cf(3/7)
2/7 = 0.285714286 : 0.428571428 = 3/7
cf(3/7) = 2, 3 → 3, 2 = cf(2/7)
3/7 = 0.428571429 : 0.285714286 = 2/7
cf(4/7) = 1, 1, 3 → 3, 1, 1 → 3, 2 = cf(2/7)
4/7 = 0.571428571 : 0.285714286 = 2/7
cf(5/7) = 1, 2, 2 → 2, 2, 1 → 2, 3 = cf(3/7)
5/7 = 0.714285714 : 0.428571429 = 3/7
cf(6/7) = 1, 6 → 6, 1 → 7 = cf(1/7)
6/7 = 0.857142857 : 0.142857143 = 1/7
cf(3/8) = 2, 1, 2 → 2, 1, 2 = cf(3/8)
0.375 : 0.375
cf(5/8) = 1, 1, 1, 2 → 2, 1, 1, 1 → 2, 1, 2 = cf(3/8)
0.625 : 0.375
cf(7/8) = 1, 7 → 7, 1 → 8 = cf(1/8)
0.875 : 0.125
cf(2/9) = 4, 2 → 2, 4 = cf(4/9)
0.222222222 : 0.444444444
cf(4/9) = 2, 4 → 4, 2 = cf(2/9)
0.444444444 : 0.222222222
And if you plot x = a1/b1 and y = (a2/b2 * 2) on a fract-L, that is, a graph whose horizontal and vertical arms represent 0 to 1, you get the fractal right at the beginning:
Fract-L for x = a1/b1 and y = (a2/b2 * 2), where a2/b2 is generated from reversed(cf(a1/b1))
You need to use (a2/b2 * 2) because a2/b2 from reversed(cf(a1/b1)) is always <= 0.5, so using raw a2/b2 generates this graph:

Fract-L for x = a1/b1 and y = a2/b2 (i.e. a2/b2 is unadjusted)
Why is it always true that a2/b2 <= 0.5? For two reasons. First, a/b > 0.5 always generate continued fractions that start with 1, like cf(2/3) = 1, 2 or cf(3/4) = 1, 3 or cf(3/5) = 1, 1, 2. Second, as previously mentioned, no continued fraction ends with 1. Therefore a reversed cf(a1/b1), where the final number, n > 1, moves to the beginning, will never begin with 1 and the a2/b2 generated from reversed(cf(a1/b1)) will always be less than 0.5 (or equal to it in the solitary case of cf(1/2) = 2).
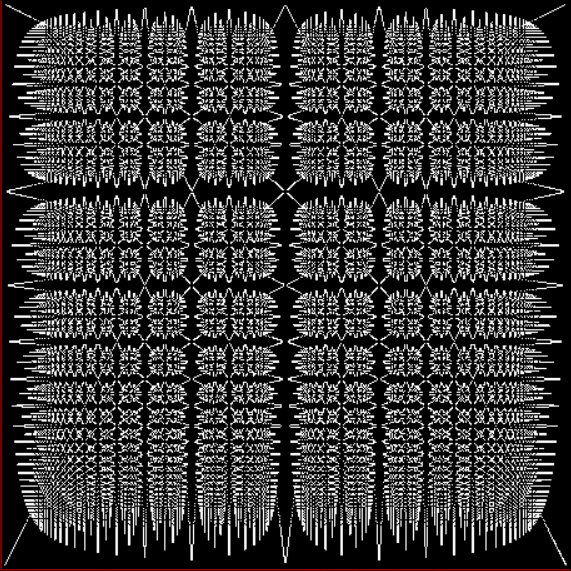
Now let's look at the development of the fractal as a1/b1 uses larger and larger denominators:

Fract-L for x = a1/b1 and y = (a2/b2 * 2) for a1/b1 <= 6/7
Fract-L for for a1/b1 <= 14/15
Fract-L for a1/b1 <= 30/31
Fract-L for a1/b1 <= 62/63
Fract-L for a1/b1 <= 126/127
Fract-L for a1/b1 <= 254/255
Fract-L for a1/b1 <= 357/358
Fract-L for a1/b1 <= 467/468
Animated fract-L for x = a1/b1 and y = (a2/b2 * 2) (animated at ezGif)
The fractal changes subtly when you restrict the b1 of a1/b1 in some way, say using multiples of 2, 3, 4, 5…:
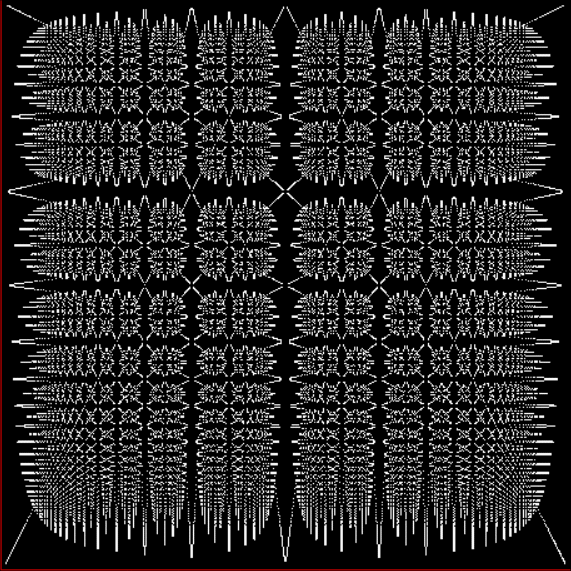
Fract-L for x = a1/b1 and y = (a2/b2 * 2) for b1 = n = 2, 3, 4, 5, 6, 7, 8…
Fract-L for b1 = 2n = 2, 4, 6, 8, 10…
Fract-L for b1 = 3n = 3, 6, 9, 12, 15…
Fract-L for b1 = 4n
Fract-L for b1 = 5n
Fract-L for b1 = 6n
Animated fract-L for b1 = 1n..12n (animated at ezGif)
Finally, here are fract-Ls when b1 is a triangular, square, hexagonal or octagonal number:
Fract-L for x = a1/b1 and y = (a2/b2 * 2) for triangular(b1) = 3, 6, 10, 15, 21, 28,…
Fract-L for square(b1) = 4, 9, 16, 25, 36, 49,…
Fract-L for hexagonal(b1) = 6, 15, 28, 45, 66, 91,…
Fract-L for octagonal(b1) = 8, 21, 40, 65, 96, 133,…
Elsewhere Other-Accessible…
• Back to Drac’ — a parallel pun for a pre-previous fractal
• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the limestone fractal
If reading continually reteaches you how to think, television is a perpetual anesthetic. Philosophy, history, complex thought are all impossible on the tube: “Its form works against the content.” — Noah McCormack, “We Used to Read Things in This Country”, The Baffler #81, November 2025

“Descending Toward the Moon” (1951) by Chesley Bonestell (1888–1986)
As Reform seeks a statement victory in Gorton and Denton, with a candidate who has made dog-whistle nativism his calling card, Manchester has again become a political crucible. […] As Nigel Farage’s intellectual outriders speak of a “politics of home”, which casts doubt over certain citizens’ right to be considered British, a billionaire tax exile in Monaco has added grist to their mill. — “Guardian view on Sir Jim Ratcliffe: Britain does not need political lectures from a billionaire tax exile”, The Guardian, 12ii26
This is the surpassingly special Stern-Brocot sequence:
0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, … (A002487 at the Online Encyclopedia of Integer Sequences)
And why is the sequence special? Because if you take successive pairs of the apparently arbitrarily varying numbers, you get every rational fraction in its simplest form exactly once. So 1/2, 2/3, 6/11 and 502/787 appear once and then never again. And so do 2/1, 3/2, 11/6 and 787/502. Et cetera, ad infinitum. If you map the Stern-Brocot sequence against the related Calkin-Wilk sequence, which has the same “all-simplest-fractions-exactly-once” properties, you can create this fractal, which I call a limestone fractal or gryke fractal:

Gryke fractal by mapping Stern-Brocot sequence against Calkin-Wilf sequence
The graph is what I call a Fract-L, because the lines for the x,y coordinates create an L. Each coordinate runs from 0 to 1, with the x set by the fraction from the Stern-Brocot sequence and the y set by the fraction from the Calkin-Wilf sequence (if a > b in a/b, use the conversion 1/(a/b) = b/a). But you can also find interesting patterns by mapping the Stern-Brocot sequence against itself. That is, you use two Stern-Brocot sequences that start in different places. Now, there are complicated ways to create the Stern-Brocot sequence using mathematical trees and sequential algorithms and so on. But there’s also an astonishingly simple way, a formula created by the Israeli mathematician Moshe Newman. If (a,b) is one pair of successive numbers in the sequence, the next pair (a,b) is found like this:
c = b
b = (2 * int(a/b) + 1) * b – a
a = c
This means that you can seed a Stern-Brocot sequence with any (correctly simplified) a/b and it will continue in the right way. If the two SB-sequences for x and y are both seeded with (0,1), you get this 45° line, because each successive a/b for (x,y) is identical:
Stern-Brocot pairs seeded with x ← (0,1) and y ← (0,1)
The further you extend the sequences, the less broken the 45° line will appear, because the points determined by a/b for x and y will get closer and closer together (but the line will never be solid, because any two rationals are separated by an infinity of irrationals). Now try offsetting the SB-sequences for x,y by using different seeds. Different fractal patterns appear, which all appear to be subsets (or fractions) of the limestone fractal above (see animated gif below):
Stern-Brocot pairs seeded with x ← (0,1) and y ← (1,1)
x ← (0,1) and y ← (1,2)
x ← (0,1) and y ← (1,3)
x ← (0,1) and y ← (2,3)
x ← (0,1) and y ← (3,4)
x ← (0,1) and y ← (6,7)
x ← (1,2) and y ← (1,9)
x ← (1,4) and y ← (1,6)
x ← (1,7) and y ← (1,8)
x ← (2,3) and y ← (4,5) — apparently identical to x ← (1,4) and y ← (1,6) above
x ← (26,25) and y ← (1,10)
Gryke fractal compared with Stern-Brocot-pair patterns (animated at ezGif)
And here’s what happens when the seed-fractions for x run from 1/3 to 12/13, while the seed-fraction for y is held constant at 1/23:
x ← (1,13) and y ← (1,23)
x ← (2,13) and y ← (1,23)
x ← (3,13) and y ← (1,23)
x ← (4,13) and y ← (1,23)
x ← (5,13) and y ← (1,23)
x ← (6,13) and y ← (1,23)
x ← (7,13) and y ← (1,23)
x ← (8,13) and y ← (1,23)
x ← (9,13) and y ← (1,23)
x ← (10,13) and y ← (1,23)
x ← (11,13) and y ← (1,23)
x ← (12,13) and y ← (1,23)
Animated gif for x ← (n,13) and y ← (1,23) (animated at ezGif)
Previously Pre-Posted
• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the fractal
Like mine, the veins of these that slumber
Leapt once with dancing fires divine;
The blood of all this noteless number
Ran red like mine.
How still, with every pulse in station,
Frost in the founts that used to leap,
The put to death, the perished nation,
How sound they sleep!
These too, these veins which life convulses,
Wait but a while, shall cease to bound;
I with the ice in all my pulses
Shall sleep as sound.
• A.E. Housman, “XX” in More Poems (1936)
Elsewhere Other-Accessible…
Serendipity in some simplification statistics. That’s what I encountered the other day. I was looking at the ways to simplify this set of fractions:
1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, 3/6, 4/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 1/11, 2/11, 3/11, …
The underlined fractions are not in their simplest possible form. For example, 2/4 simplifies to 1/2, 2/6 to 1/3, 3/6 to 1/2, and so on:
1/2, 1/3, 2/3, 1/4, 2/4 → 1/2, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6 → 1/3, 3/6 → 1/2, 4/6 → 2/3, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8 → 1/4, 3/8, 4/8 → 1/2, 5/8, 6/8 → 3/4, 7/8, 1/9, 2/9, 3/9 → 1/3, 4/9, 5/9, 6/9 → 2/3, 7/9, 8/9, 1/10, 2/10 → 1/5, 3/10, 4/10 → 2/5, 5/10 → 1/2, 6/10 → 3/5, 7/10, 8/10 → 4/5, 9/10, 1/11, 2/11, 3/11, …
I counted the number of times the simplest possible fractions occurred when simplifying all fractions a/b for (b = 2..n, a = 1..b-1), then displayed the stats as a graph running from 0/1 to 1/1. And there was serendipity in these simplification statistics, because a fractal had appeared:
Graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)
It’s interesting to work out what fractions appear where. For example, the peak in the middle is 1/2, but what are the next-highest peaks on either side? The answers are more obvious in the colored version of the graph:
Colored graph for count of simplest possible fractions
Key: n/2, n/3, n/4, n/5, n/6, n/7
The line for 1/2 is red, the lines for 1/3 and 2/3 in light green, the lines for 1/4 and 3/4 in yellow, and so on. But those graphs appear in an equilateral triangle, as it were. The fractals get easier to see in the full-sized versions of these widened graphs:
Widened graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)
(click for full size)
Widened and colored graph for count of simplest possible fractions
(click for full size)
In the wake of the spread of Protestantism, the literacy rates in the newly reforming populations in Britain, Sweden, and the Netherlands surged past more cosmopolitan places like Italy and France. Motivated by [the demands of] eternal salvation, parents and leaders made sure the children learned to read. […] The Protestant impact on literacy and education can still be observed today in the differential impact of Protestant vs. Catholic missions in Africa and India. In Africa, regions with early Protestant missions at the beginning of the Twentieth Century (now long gone) are associated with literacy rates that are about 16 percentage points higher, on average, than those associated with Catholic missions. In some analyses, Catholics have no impact on literacy at all unless they faced direct competition for souls from Protestant missions. These impacts can also be found in early twentieth-century China.