Category Archives: Geometry

Second Whirled Warp

by in Geometry, Mathematics and tagged , , , , , , , , | Leave a comment

In “First Whirled Warp”, I looked at the paths traced by the midpoint of two points moving at varying speeds around the perimeter of a circle or polygon. Now I wanted to look at the midpoint of two points moving on the perimeter of a star. Suppose the star looks like this:

Four-pointed star

If the two points start at the same vertex and one point is moving 1/2 as fast as the other, the midpoint traces a shape like the head of a fox:

Fox-head from midpoint of two points moving in speed-ratio 1/2 : 1 (or 1 : 2)

If one point is moving 1/3 as fast (or 3x faster), the trace looks like this:

Midpoint of two points moving in speed-ratio 1/3 : 1

And if the points are moving -1/3 : 1, that is, in opposite directions (one clockwise, one widdershins):

Speed-ratio -1/3 : 1

And you can adjust all pixels outward so that the outer vertices of the star lie on the perimeter of a circle:

Speed-ratio -1/3 : 1 (circular)

Here are more traces created by the midpoint of two points moving around the perimeter of a four-pointed star:

Speed-ratio 1/5 : 1

Speed-ratio 3/5 : 1

↓

Speed-ratio 3/5 : 1 (circular)

Speed-ratio -3/7 : 1/3

↓

Speed-ratio -3/7 : 1/3 (circular)

Speed-ratio 7/3 : 6/7

↓

Speed-ratio 7/3 : 6/7 (circular)

Speed-ratio -7/3 : 6/7

↓

Speed-ratio -7/3 : 6/7 (circular)

If the star is adjusted like this:

Variant on four-pointed star

You can get mid-traces like this:

Speed-ratio -1/7 : 1 (adjusted star)

↓

Speed-ratio -1/7 : 1 (adjusted star) (circular)

Here’s a three-pointed star:

Speed-ratio -4/5 : 1 (3p star)

↓

Speed-ratio -4/5 : 1 (3p star) (circular)

And some five-pointed stars:

Speed-ratio 2/7 : 1 (5p star)

↓

Speed-ratio 2/7 : 1 (5p star) (circular)

Speed-ratio -7/5 : 3/7 (5p star)

↓

Speed-ratio -7/5 : 3/7 (5p star) (circular)

Previously Pre-Posted

• First Whirled Warp — an earlier look at points performativizing on perimeters

Trigging Triangles

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , , , | Leave a comment

A fractal is a shape in which a part looks like the whole. Trees are fractals. And lungs. And clouds. But there are man-made fractals too and probably the most famous of them all is the Sierpiński triangle, invented by the Polish mathematician Wacław Sierpiński (1882-1969):

Sierpiński triangle

There are many ways to create a Sierpiński triangle, but one of the simplest is to trace all possible routes followed by a point jumping halfway towards the vertices of an equilateral triangle. If you mark the endpoint of the jumps, the Sierpiński triangle appears as the routes get longer and longer, like this:

Point jumping 1/2 way towards vertices of an equilateral triangle (animated)

Once you’ve created a Sierpiński triangle like that, you can play with it. For example, you can use simple trigonometry to stretch the triangle into a circle:

Sierpiński triangle to circle stage #1

Sierpiński triangle to circle #2

Sierpiński triangle to circle #3

Sierpiński triangle to circle #4

Sierpiński triangle to circle #5

Sierpiński triangle to circle #6

Sierpiński triangle to circle #7

Sierpiński triangle to circle #8

Sierpiński triangle to circle #9

Sierpiński triangle to circle #10

Sierpiński triangle to Sierpiński circle (animated)

But the trigging of the triangle can go further. You can expand the Sierpiński circle further, like this:

Sierpiński circle expanded

Or shrink the Sierpiński triangle like this:

Shrinking Sierpiński triangle stage #1

Shrinking Sierpiński triangle #2

Shrinking Sierpiński triangle #3

Shrinking Sierpiński triangle #4

Shrinking Sierpiński triangle #5

Shrinking Sierpiński triangle #6

Shrinking Sierpiński triangle (animated)

You can also create new shapes using the jumping-point technique. Suppose that, as the point is jumping, you adjust its position outwards into the circumscribed circle whenever it lands within the boundaries of the governing triangle. But if the point lands outside those boundaries, you leave it alone. Using this adapted technique, you get a shape like this:

Adjusted Sierpiński circle

And if the point is swung by 60° after it’s adjusted into the circle, you get a shape like this:

Adjusted Sierpiński circle (60° swing)

Here are some animated gifs showing these shapes rotating in a full circle at various speeds:

Adjusted Sierpiński circle (swinging animation) (fast)

Adjusted Sierpiński circle (swinging animation) (medium)

Adjusted Sierpiński circle (swinging animation) (slow)

Square Routes Re-Re-Re-Re-Re-Re-Revisited

by in Fractals, Geometry, Mathematics, Pentagons, Polygons, Squares, Triangles and tagged , , , , , , , , | Leave a comment

Suppose you trace all possible routes followed by a point inside a triangle jumping halfway towards one or another of the three vertices of the triangle. If you mark each jump, you get a famous geometrical shape called the Sierpiński triangle (or Sierpiński sieve).

Sierpiński triangle found by tracing all possible routes for a point jumping halfway towards the vertices of a triangle

The Sierpiński triangle is a fractal, because it contains copies of itself at smaller and smaller scales. Now try the same thing with a square. If you trace all possible routes followed by a point inside a square jumping halfway towards one or another of the four vertices of the square, you don’t get an obvious fractal. Instead, the interior of the square fills steadily (and will eventually be completely solid):

Routes of a point jumping halfway towards vertices of a square

Try a variant. If the point is banned from jumping towards the same vertex twice or more in a row, the routes trace out a fractal that looks like this:

Ban on choosing same vertex twice or more in a row

If the point is banned from jumping towards the vertex one place anti-clockwise of the vertex it’s just jumped towards, you get a fractal like this:

Ban on jumping towards vertex one place anti-clockwise of previously chosen vertex

And if the point can’t jump towards two places clockwise or anti-clockwise of the currently chosen vertex, this fractal appears (called a T-square fractal):

Ban on jumping towards the vertex diagonally opposite of the previously chosen vertex

That ban is equivalent to banning the point from jumping from the vertex diagonally opposite to the vertex it’s just jumped towards. Finally, here’s the fractal created when you ban the point from jumping towards the vertex one place clockwise of the vertex it’s just jumped towards:

Ban on jumping towards vertex one place clockwise of previously chosen vertex

As you can see, the fractal is a mirror-image of the one-place-anti-clockwise-ban fractal.

I discovered the ban-construction of those fractals more than twenty years ago. Then I found that I was re-discovering the same fractals when I looked at what first seemed like completely different ways of constructing fractals. There are lots of different routes to the same result. I’ve recently discovered yet another route. Let’s try what seems like an entirely different way of constructing fractals. Take a square and erect four new half-sized squares, sq1, sq2, sq3, sq4, on each corner. Then erect three more quarter-sized squares on the outward facing corners of sq1, sq2, sq3 and sq4. Carry on doing that and see what happens at the end when you remove all the previous stages of construction:

Animation of the new construction

Animation in black-and-white

It’s the T-square fractal again. Now try rotating the squares you add at stage 3 and see what happens (the rotation means that two new squares are added on adjacent outward-facing corners and one new square on the inward-facing corner):

Animation of the construction

It’s the one-place-clockwise-ban fractal again. Now try rotating the squares two places, so that two new squares are added on diagonally opposite outward-facing corners and one new square on the inward-facing corner:

Animation of the construction

It’s the same-vertex-ban fractal again. Finally, rotate squares one place more:

Animation of the construction

It’s the one-place-clockwise-ban fractal again. And this method isn’t confined to squares. Here’s what happens when you add 5/8th-sized triangles to the corners of triangles:

Animation of the construction

And here’s what happens when you add 5/13th-sized pentagons to the corners of pentagons:

Animation of the construction

Finally, here’s a variant on that pentagonal fractal (adding two rather than four pentagons at stage 3 and higher):

Animation of the construction

Previously pre-posted (please peruse):

• Square Routes
• Square Routes Revisited
• Square Routes Re-Revisited
• Square Routes Re-Re-Revisited
• Square Routes Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Re-Revisited

The Hex Fractor #3

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , | Leave a comment

In “Diamonds to Dust”, I showed how the Mitsubishi logo could be turned into a fractal, like this:

The Mitsubishi diamonds (source)

↓

↓

Mitsubishi logo to fractal (animated)

Now I want to look at another famous symbol and its fractalization. Here’s the symbol, the hexagram:

Hexagram, a six-pointed star

The hexagram can be dissected into twelve equilateral triangles like this:

Hexagram dissected into 12 equilateral triangles

If each triangle in the dissection is replaced by a hexagram, then the hexagram is dissected again into twelve triangles, you get a famous fractal, the Koch snowflake:

The Koch snowflake

The Koch snowflake again

Hexagram to Koch snowflake (animated)

If you color the triangles, you get something like this:

Colored hexagram to fractal (animated)

Of course, this is a very inefficient way to create a Koch snowflake, because the interior hexagrams consume processing time while not contributing to the fractal boundary of the snowflake. But in a way you can fully fractalize the hexagram if you draw only the point at the center of each triangle and then color it according to how many times the pixel in question has been drawn on before. To see how this works, first look at what happens when the center-points are represented in white:

White center-points (animated)

And here’s the fully fractalized hexagram, with colored center-points:

Colored center-points (animated)

Previously Pre-Posted…

• The Hex Fractor #1 — hexagons and fractals
• The Hex Fractor #2 — hexagons and fractals again
• Diamonds to Dust — turning the Mitsubishi logo into a fractal

Trim Pickings

by in Fractals, Geometry, Mathematics, Rep-Tiles, Triangles and tagged , , , , , , | Leave a comment

Here is an equilateral triangle divided into nine smaller equilateral triangles:

Rep-9 equilateral triangle

The triangle is a rep-tile — it’s tiled with repeating copies of itself. In this case, it’s a rep-9 triangle. Each of the nine smaller triangles can obviously be divided in their turn:

Rep-81 equilateral triangle

Rep-729 equilateral triangle

Rep-729 equilateral triangle again

Rep-6561 equilateral triangle

Rep-9 triangle repeatedly subdividing (animated)

How try trimming the original rep-9 triangle, picking one of the trimmings, and repeating in finer detail. If you choose six triangles in this pattern, you can create a symmetrical braided fractal:

Triangular fractal stage 1

Triangular fractal #2

Triangular fractal #3

Triangular fractal #3 (cleaning up)

Triangular fractal #3 (cleaning up more)

Triangular fractal #4

Triangular fractal #5

Triangular fractal #6

Triangular fractal (animated)

But this fractal using a three-triangle trim-picking isn’t symmetrical:

Trim-picking #1

Trim-picking #2

Trim-picking #3

Trim-picking #4

Trim-picking #5

To make it symmetric, you have to delay the trim, using the full rep-9 trim for the first stage:

Delayed trim-picking #1

Delayed trim-picking #2

Delayed trim-picking #3

Delayed trim-picking #4

Delayed trim-picking #5

Delayed trim-picking #6 (with first two stages as rep-9)

Delayed trim-picking (animated)

Here are some more delayed trim-pickings used to created symmetrical patterns:

Polykoch (Kontinued)

by in Fractals, Geometry, Mathematics, Polygons, Squares, Triangles and tagged , , , , , , , , , , | Leave a comment

In “Polykoch!”, I looked at variants on the famous Koch snowflake, which is created by erecting new triangles on the sides of an equilaternal triangle, like this:

Koch snowflake #1

Koch snowflake #2

Koch snowflake #3

Koch snowflake #4

Koch snowflake #5

Koch snowflake #6

Koch snowflake #7

Koch snowflake (animated)

One variant is simple: the new triangles move inward rather than outward:

Inverted Koch snowflake #1

Inverted Koch snowflake #2

Inverted Koch snowflake #3

Inverted Koch snowflake #4

Inverted Koch snowflake #5

Inverted Koch snowflake #6

Inverted Koch snowflake #7

Inverted Koch snowflake (animated)

Or you can alternate between moving the new triangles inward and outward. When they always move outward and have sides 1/5 the length of the sides of the original triangle, the snowflake looks like this:

When they move inward, then always outward, the snowflake looks like this:

And so on:

Now here’s a Koch square with its new squares moving inward:

Inverted Koch square #1

Inverted Koch square #2

Inverted Koch square #3

Inverted Koch square #4

Inverted Koch square #5

Inverted Koch square #6

Inverted Koch square (animated)

And here’s a pentagon with squares moving inwards on its sides:

Pentagon with squares #1

Pentagon with squares #2

Pentagon with squares #3

Pentagon with squares #4

Pentagon with squares #5

Pentagon with squares #6

Pentagon with squares (animated)

And finally, an octagon with hexagons on its sides. First the hexagons move outward, then inward, then outward, then inward, then outward:

Octagon with hexagons #1

Octagon with hexagons #2

Octagon with hexagons #3

Octagon with hexagons #4

Octagon with hexagons #5

Octagon with hexagons (animated)

Polykoch!

by in Fractals, Geometry, φ, Mathematics, Pentagons, Phi, Squares, Triangles and tagged , , , , , , , , , | Leave a comment

This is how you form the famous Koch snowflake, in which at each stage you erect a new triangle on the middle of each line whose sides are 1/3 the length of the line:

Koch snowflake #1

Koch snowflake #2

Koch snowflake #3

Koch snowflake #4

Koch snowflake #5

Koch snowflake #6

Koch snowflake #7

Koch snowflake (animated)

Here’s a variant of the Koch snowflake, with new mid-triangles whose sides are 1/2 the length of the lines:

Koch snowflake (1/2 side) #1

Koch snowflake (1/2 side) #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Koch snowflake (1/2 side) (animated)

But why stop at triangles? This is a Koch square, in which at each stage you erect a new 1/3 square on the middle of each line:

Koch square #1

Koch square #2

Koch square #3

Koch square #4

Koch square #5

Koch square #6

Koch square (animated)

And a Koch pentagon, in which at each stage you erect a pentagon on the middle of each line whose sides are 1 – (1/φ^2 * 2) = 0·236067977… the length of the line (I used 55/144 as an approximation of 1/φ^2):

Koch pentagon (side 55/144) #1

Koch pentagon #2

Koch pentagon #3

Koch pentagon #4

Koch pentagon #5

Koch pentagon #6

Koch pentagon (animated)

In this close-up, you can see how precisely the sprouting pentagons kiss at each stage:

Koch pentagon (close-up) #1

Koch pentagon (close-up) #2

Koch pentagon (close-up) #3

Koch pentagon (close-up) #4

Koch pentagon (close-up) #5

Koch pentagon (close-up) #6

Koch pentagon (close-up) (animated)

Period Panes

by in Arithmetic, Base Behavior, Circles, Geometry, Mathematics, Reciprocals and tagged , , , , , , , , , , , , , , , , , , , , , | Leave a comment

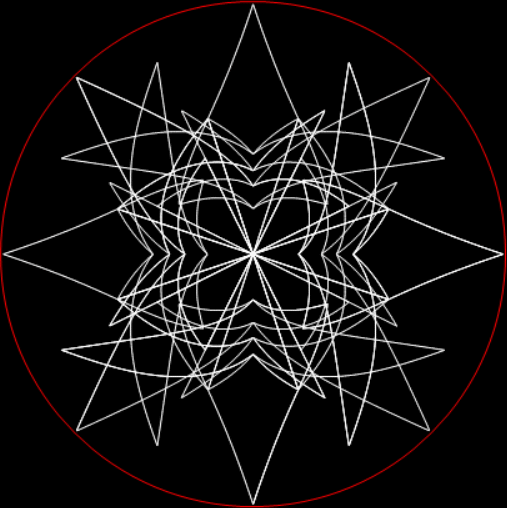
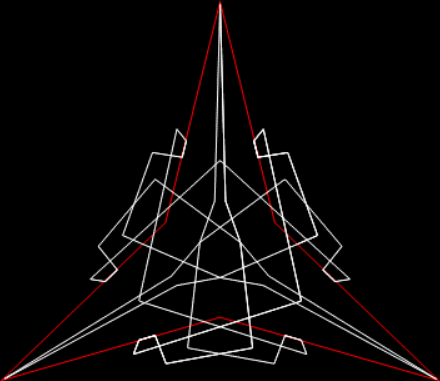
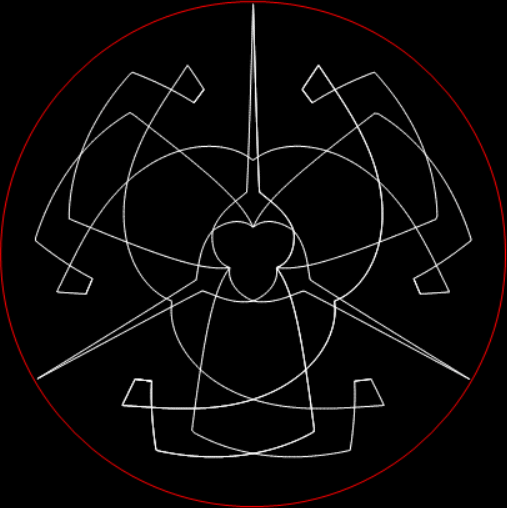
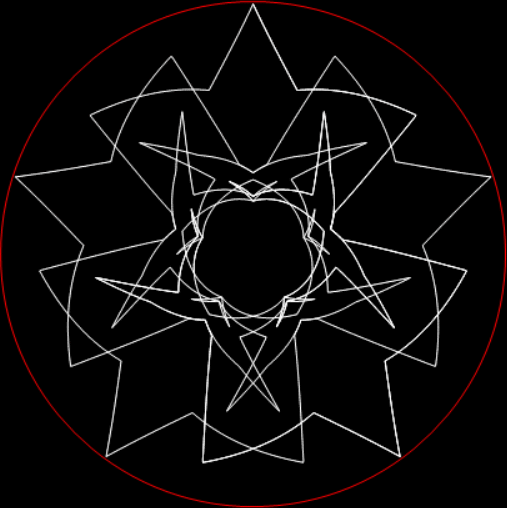
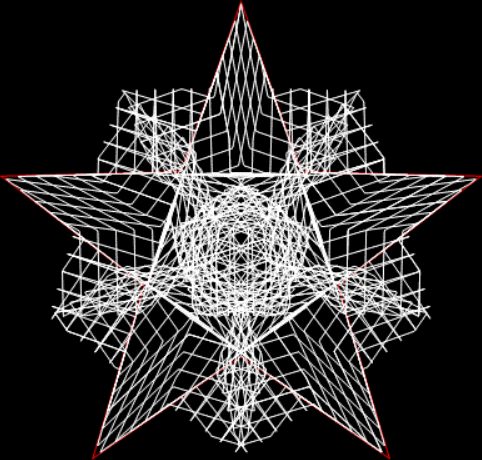
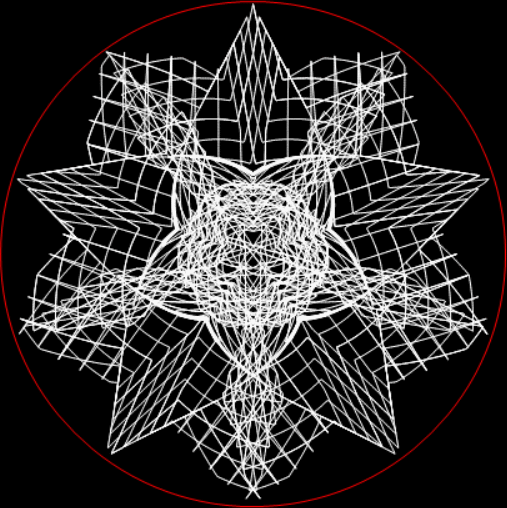
In his Penguin Dictionary of Curious and Interesting Numbers (1986), David Wells says that 142857 is “beloved of all recreational mathematicians”. He then says it’s the decimal period of the reciprocal of the fourth prime: “1/7 = 0·142857142857142…” And the reciprocal has maximum period. There are 6 = 7-1 digits before repetition begins, unlike the earlier prime reciprocals:


1/2 = 0·5
1/3 = 0·333...
1/5 = 0·2
1/7 = 0·142857 142857 142...

In other words, all possible remainders appear when you calculate the decimals of 1/7:


1*10 / 7 = 1 remainder 3 → 0·1
3*10 / 7 = 4 remainder 2 → 0·14
2*10 / 7 = 2 remainder 6 → 0·142
6*10 / 7 = 8 remainder 4 → 0·1428
4*10 / 7 = 5 remainder 5 → 0·14285
5*10 / 7 = 7 remainder 1 → 0·142857
1*10 / 7 = 1 remainder 3 → 0·142857 1
3*10 / 7 = 4 remainder 2 → 0·142857 14
2*10 / 7 = 2 remainder 6 → 0·142857 142...

That happens again with 1/17 and 1/19, but Wells says that “surprisingly, there is no known method of predicting which primes have maximum period.” It’s a simple question that involves some deep mathematics. Looking at prime reciprocals is like peering through a small window into a big room. Some things are easy to see, some are difficult and some are presently impossible.

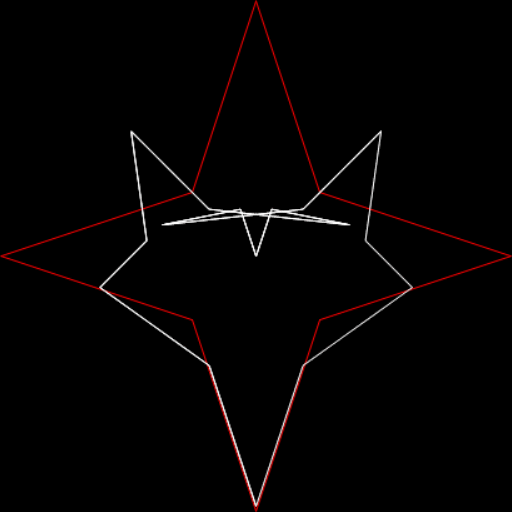
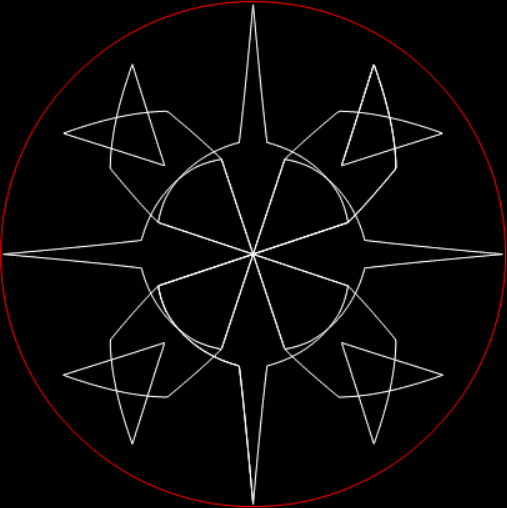
In his discussion of 142857, Wells mentions one way of peering through a period pane: “The sequence of digits also makes a striking pattern when the digits are arranged around a circle.” Here is the pattern, with ten points around the circle representing the digits 0 to 9:

The digits of 1/7 = 0·142857142…

But I prefer, for further peers through the period-panes, to create the period-panes using remainders rather than digits. That is, the number of points around the circle is determined by the prime itself rather than the base in which the reciprocal is calculated:

The remainders of 1/7 = 1, 3, 2, 6, 4, 5…

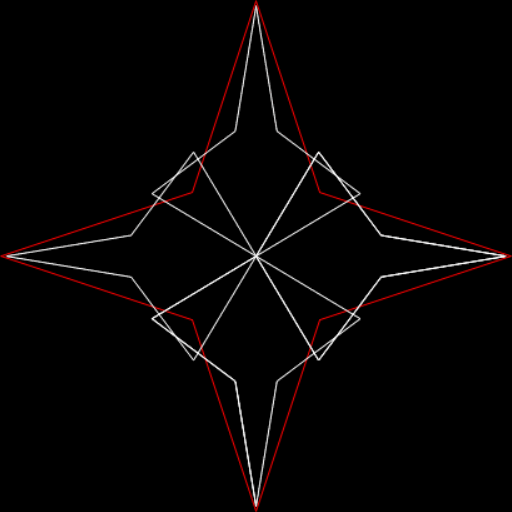
Period-panes can look like butterflies or bats or bivalves or spiders or crabs or even angels. Try the remainders of 1/13. This prime reciprocal doesn’t have maximum period: 1/13 = 0·076923 076923 076923… So there are only six remainders, creating this pattern:

remainders(1/13) = 1, 10, 9, 12, 3, 4

The multiple 2/13 has different remainders and creates a different pattern:

remainders(2/13) = 2, 7, 5, 11, 6, 8

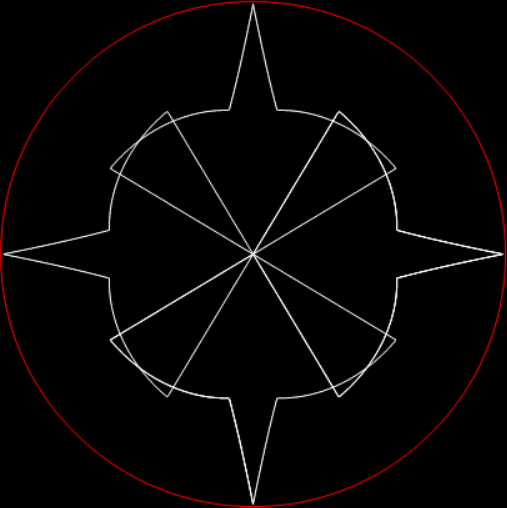
But 1/17, 1/19 and 1/23 all have maximum period and yield these period-panes:

remainders(1/17) = 1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12

remainders(1/19) = 1, 10, 5, 12, 6, 3, 11, 15, 17, 18, 9, 14, 7, 13, 16, 8, 4, 2

remainders(1/23) = 1, 10, 8, 11, 18, 19, 6, 14, 2, 20, 16, 22, 13, 15, 12, 5, 4, 17, 9, 21, 3, 7

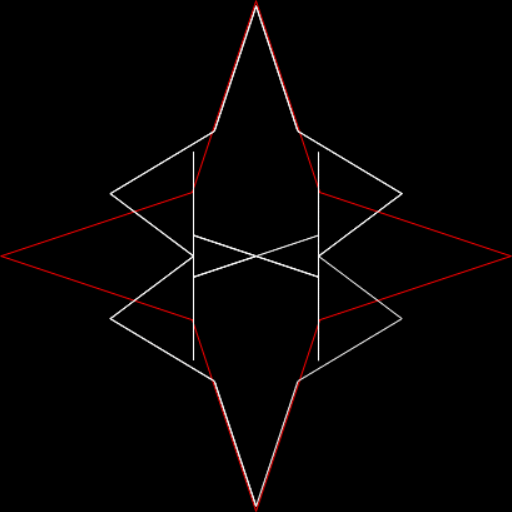
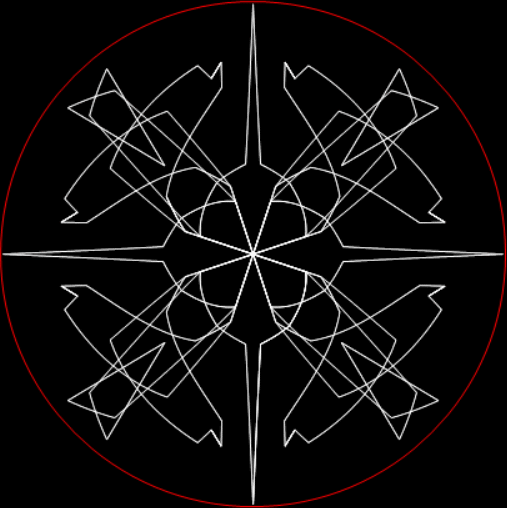
It gets mixed again with the prime 73, which doesn’t have maximum period and yields a plethora of period-panes (some patterns repeat with different n * 1/73, so I haven’t included them):

remainders(1/73)

remainders(2/73)

remainders(3/73)

remainders(4/73)

remainders(5/73)

remainders(6/73)

remainders(9/73)

remainders(11/73) (identical to pattern of 5/73)

remainders(12/73)

remainders(18/73)

101 yields a plethora of period-panes, but they’re variations on a simple theme. They look like flapping wings in this animated gif:

remainders of n/101 (animated)

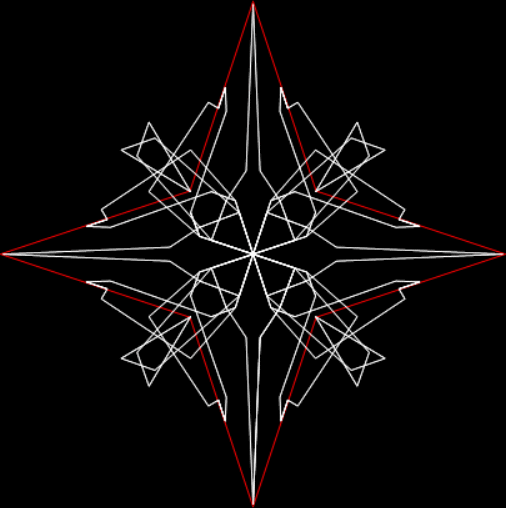
The remainders of 137 yield more complex period-panes:

remainders of n/137 (animated)

And what about different bases? Here are period-panes for the remainders of 1/17 in bases 2 to 16:

remainders(1/17) in base 2

remainders(1/17) in b3

remainders(1/17) in b4

remainders(1/17) in b5

remainders(1/17) in b6

remainders(1/17) in b7

remainders(1/17) in b8

remainders(1/17) in b9

remainders(1/17) in b10

remainders(1/17) in b11

remainders(1/17) in b12

remainders(1/17) in b13

remainders(1/17) in b14

remainders(1/17) in b15

remainders(1/17) in b16

remainders(1/17) in bases 2 to 16 (animated)

But the period-panes so far have given a false impression. They’ve all been symmetrical. That isn’t the case with all the period-panes of n/19:

remainders(1/19) in b2

remainders(1/19) in b3

remainders(1/19) in b4 = 1, 4, 16, 7, 9, 17, 11, 6, 5 (asymmetrical)

remainders(1/19) in b5 = 1, 5, 6, 11, 17, 9, 7, 16, 4 (identical pattern to that of b4)

remainders(1/19) in b6

remainders(1/19) in b7

remainders(1/19) in b8

remainders(1/19) in b9

remainders(1/19) in b10 (identical pattern to that of b2)

remainders(1/19) in b11

remainders(1/19) in b12

remainders(1/19) in b13

remainders(1/19) in b14

remainders(1/19) in b15

remainders(1/19) in b16

remainders(1/19) in b17

remainders(1/19) in b18

remainders(1/19) in bases 2 to 18 (animated)

Here are a few more period-panes in different bases:

remainders(1/11) in b2

remainders(1/11) in b7

remainders(1/13) in b6

remainders(1/43) in b6

remainders in b2 for reciprocals of 29, 37, 53, 59, 61, 67, 83, 101, 107, 131, 139, 149 (animated)

And finally, to performativize the pun of “period pane”, here are some period-panes for 1/29, whose maximum period will be 28 (NASA says that the “Moon takes about one month to orbit Earth … 27.3 days to complete a revolution, but 29.5 days to change from New Moon to New Moon”):

remainders(1/29) in b4

remainders(1/29) in b5

remainders(1/29) in b8

remainders(1/29) in b9

remainders(1/29) in b11

remainders(1/29) in b13

remainders(1/29) in b14

remainders(1/29) in various bases (animated)