Summer Sets (and Truncated Triangulars)

by in Arithmetic, Integer Sequences, Mathematics, Triangular Numbers and tagged , , , | Leave a comment

Here is the sequence of triangular numbers, created by summing consecutive integers from 1 (i.e., 1+2+3+4+5…):


1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431, 1485, 1540, 1596, 1653, 1711, 1770, 1830, 1891, 1953, 2016, 2080, 2145, 2211, 2278, 2346, 2415, 2485, 2556, 2628, 2701, 2775, 2850, 2926, 3003, 3081, 3160, 3240, 3321, 3403, 3486, 3570, 3655, 3741, 3828, 3916, 4005, 4095, 4186, 4278, 4371, 4465, 4560, 4656, 4753, 4851, 4950, 5050, 5151, 5253, 5356, 5460, 5565, 5671, 5778, 5886, 5995...

And here is a sequence of truncated triangulars, created by summing consecutive integers from 15 (i.e., 15+16+17+18+19…):


15, 31, 48, 66, 85, 105, 126, 148, 171, 195, 220, 246, 273, 301, 330, 360, 391, 423, 456, 490, 525, 561, 598, 636, 675, 715, 756, 798, 841, 885, 930, 976, 1023, 1071, 1120, 1170, 1221, 1273, 1326, 1380, 1435, 1491, 1548, 1606, 1665, 1725, 1786, 1848, 1911, 1975, 2040, 2106, 2173, 2241, 2310, 2380, 2451, 2523, 2596, 2670, 2745, 2821, 2898, 2976, 3055, 3135, 3216, 3298, 3381, 3465, 3550, 3636, 3723, 3811, 3900, 3990, 4081, 4173, 4266, 4360, 4455, 4551, 4648, 4746, 4845, 4945, 5046, 5148, 5251, 5355, 5460, 5566, 5673, 5781...

It’s obvious that the sequences are different at each successive step: 1 ≠ 15, 3 ≠ 31, 6 ≠ 48, 10 ≠ 66, 21 ≠ 85, and so on. But seven numbers occur in both sequences: 15, 66, 105, 171, 561, 1326 and 5460. And that’s it — 7 is the 14-th entry in A309507 at the Encyclopedia of Integer Sequences:


0, 1, 1, 1, 3, 3, 1, 2, 5, 3, 3, 3, 3, 7, 3, 1, 5, 5, 3, 7, 7, 3, 3, 5, 5, 7, 7, 3, 7, 7, 1, 3, 7, 7, 11, 5, 3, 7, 7, 3, 7, 7, 3, 11, 11, 3, 3, 5, 8, 11, 7, 3, 7, 15, 7, 7, 7, 3, 7, 7, 3, 11, 5, 3, 15, 7, 3, 7, 15, 7, 5, 5, 3, 11, 11, 7, 15, 7, 3, 9, 9, 3, 7 — A309507

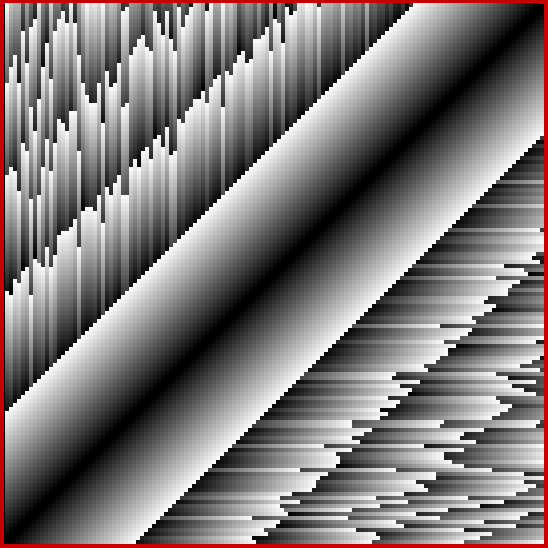
I decided to take create graphs of shared numbers in compared sequences like this. In the 135×135 grid below, the brightness of the squares corresponds to the count of shared numbers in the sequence-pair sum(x..x+n) and sum(y..y+n), where x and y are the coordinates of each individual square. I think the grid looks like a city of skyscrapers bisected by a highway:

Count of shared numbers in sequence-pairs sum(x..x+n) and sum(y..y+n)

Note that the bright white diagonal in the grid corresponds to the sequence-pairs where x = y. Because the sequences are identical in each pair, the count of shared numbers is infinite. The grid is symmetrically reflected along the diagonal because, for example, the sequence-pair for x=12, y=43, where sum(12..12+n) is compared with sum(43..43+n), corresponds to the sequence pair for x=43, y=12, where sum(43..43+n) is compared with sum(12..12+n). The scale of brightness runs from 0 (black) to 255 (full white) and increases by 32 for each shared number in the sequence. Obviously, then, the brightness can’t increase indefinitely and some maximally bright squares will represent sequence-pairs that have different counts of shared pairs.

Now try altering the size of the step in brightness. You get grids in which the width of the central strip increases (smaller step) or decreases (bigger step). Here are grids for steps for 1, 2, 4, 8, 16, 32 and 64 (I’ve removed the bright x=y diagonal for the first few grids, because it’s too prominent against duller shades):

Brightness-step = 1

Brightness-step = 2

Brightness-step = 4

Brightness-step = 8

Brightness-step = 16

Brightness-step = 32

Brightness-step = 63

Brightness-step = 1, 2, 4, 8, 16, 32, 63 (animated)

Summery Summary

by in Language, Linguistics and tagged , , , , , , | Leave a comment

sun, n., The bright celestial object which is the chief source of natural light and heat on earth and appears to pass across the sky each day from east to west; the central body of the solar system, around which the earth and other planets orbit, and which by its changing position relative to the earth’s axis determines the seasons.

Summary

A word inherited from Germanic.

Cognate with Old Frisian sunne, sonne, senne (West Frisian sinne, North Frisian sen), Old Saxon sunna (Middle Low German sunne), Old Dutch sunna (Middle Dutch sonne, Dutch zon), Old High German sunna (Middle High German sunne, sonne, German Sonne), Old Icelandic sunna (in poetry), Gothic sunno, Crimean Gothic sune,

< a variant of the same Indo-European base as early Scandinavian (runic: Norway) solu (dative singular), Old Icelandic sól, Old Swedish, Swedish sol, Old Danish, Danish sol, Gothic sauil, and also Sanskrit svar (genitive sūraḥ), Old Avestan huuarə̄, ancient Greek ἥλιος, ἠέλιος (Doric ἀέλιος, Cretan ἀβέλιος; compare helio– comb. form), classical Latin sōl, Old Welsh houl (Welsh haul), Old Prussian saule, Lithuanian saulė, all in sense ‘sun’, and Early Irish, Irish súil eye. — Oxford English Dictionary

Froth of a Boy

by in Literature, Poetry and tagged , , , , , , , , , , , , , , , | Leave a comment

“Portrait Of A Boy” by Stephen Vincent Benét (1898-1943)

After the whipping he crawled into bed,
Accepting the harsh fact with no great weeping.
How funny uncle’s hat had looked striped red!
He chuckled silently. The moon came, sweeping
A black, frayed rag of tattered cloud before
In scorning; very pure and pale she seemed,
Flooding his bed with radiance. On the floor
Fat motes danced. He sobbed, closed his eyes and dreamed.

Warm sand flowed round him. Blurts of crimson light
Splashed the white grains like blood. Past the cave’s mouth
Shone with a large, fierce splendor, wildly bright,
The crooked constellations of the South;
Here the Cross swung; and there, affronting Mars,
The Centaur stormed aside a froth of stars.
Within, great casks, like wattled aldermen,
Sighed of enormous feasts, and cloth of gold
Glowed on the walls like hot desire. Again,
Beside webbed purples from some galleon’s hold,
A black chest bore the skull and bones in white
Above a scrawled “Gunpowder!” By the flames,
Decked out in crimson, gemmed with syenite,
Hailing their fellows with outrageous names,
The pirates sat and diced. Their eyes were moons.
“Doubloons!” they said. The words crashed gold. “Doubloons!”

• Stephen Vincent Benét at Wikipedia

Post-Performative Post-Scriptum

The title of this post is a paronomasia on the Irish idiom “broth of a boy”, which means “a lively, energetic, or highly capable boy or young man”.

Power Flip

by in Arithmetic, Base Behavior, Integer Sequences, Mathematics, Powers, Prime numbers and tagged , , , , , , , , , , , , , , | Leave a comment

12 is an interesting number in a lot of ways. Here’s one way I haven’t seen mentioned before:

12 = 3^1 * 2^2


The digits of 12 represent the powers of the primes in its factorization, if primes are represented from right-to-left, like this: …7, 5, 3, 2. But I couldn’t find any more numbers like that in base 10, so I tried a power flip, from right-left to left-right. If the digits from left-to-right represent the primes in the order 2, 3, 5, 7…, then this number is has prime-power digits too:

81312000 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2 * 13^0 * 17^0 * 19^0


Or, more simply, given that n^0 = 1:

81312000 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2


I haven’t found any more left-to-right prime-power digital numbers in base 10, but there are more in other bases. Base 5 yields at least three (I’ve ignored numbers with just two digits in a particular base):

110 in b2 = 2^1 * 3^1 (n=6)
130 in b6 = 2^1 * 3^3 (n=54)
1010 in b2 = 2^1 * 3^0 * 5^1 (n=10)
101 in b3 = 2^1 * 3^0 * 5^1 (n=10)
202 in b7 = 2^2 * 3^0 * 5^2 (n=100)
3020 in b4 = 2^3 * 3^0 * 5^2 (n=200)
330 in b8 = 2^3 * 3^3 (n=216)
13310 in b14 = 2^1 * 3^3 * 5^3 * 7^1 (n=47250)
3032000 in b5 = 2^3 * 3^0 * 5^3 * 7^2 (n=49000)
21302000 in b5 = 2^2 * 3^1 * 5^3 * 7^0 * 11^2 (n=181500)
7810000 in b9 = 2^7 * 3^8 * 5^1 (n=4199040)
81312000 in b10 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2


Post-Performative Post-Scriptum

When I searched for 81312000 at the Online Encyclopedia of Integer Sequences, I discovered that these are Meertens numbers, defined at A246532 as the “base n Godel encoding of x [namely,] 2^d(1) * 3^d(2) * … * prime(k)^d(k), where d(1)d(2)…d(k) is the base n representation of x.”

Coptic Optics

by in Aesthetics, Art, Color, History, Language and tagged , , , , , , , | Leave a comment

Coptic Cross with abbreviation Ⲓⲏ̅ⲥ̅ Ⲡⲭ̅ⲥ̅ Ⲡ̀ϣⲏⲣⲓ ⲙ̀ⲪϮ standing for Ⲓⲏⲥⲟⲩⲥ Ⲡⲓⲭ̀ⲣⲓⲥⲧⲟⲥ Ⲡ̀ϣⲏⲣⲓ ⲙ̀Ⲫ̀ⲛⲟⲩϯ,
Iêsous Piekhristos Epshêri Emefnouti, “Jesus Christ, Son of God” (see Wikipedia)

Performativizing Papyrocentricity #78

by in Book Reviews and tagged , , , , , , , , , , , , , , , | Leave a comment

Papyrocentric Performativity Presents…

• Moist and Marvellous – The Hidden World of Mosses, Neil Bell (Royal Botanical Garden Edinburgh, 2023)

• Mutton Ju: The Balls-Up in Brideshead

• Little Littérateur – Evelyn Waugh: A Life Revisited, Philip Eade (Weidenfeld & Nicolson 2016)

• Vegetarian Villan – Into the Void: From Birth to Black Sabbath and Beyond, Geezer Butler (HarperCollins 2023)

• Blood Triangle – Blood Work, Michael Connelly (1998)

• Haute Coltour – The World According to Colour: A Cultural History, James Fox (Penguin 2021)

• Heil Halitosis! – Bad Breath, David Britton (Savoy Books 2022)

The Number of the Creased

by in 666, Arithmetic, Mathematics, Number of the Beast and tagged , , , , , , , , , | Leave a comment

Here’s an idea for a story à la M.R. James. A middle-aged scholar opens some mail one morning and finds nothing inside one envelope but a strip of paper with the numbers 216348597 written on it in sinister red ink. Someone has folded the strip several times so that there are creases between groups of numbers, like this: 216|348|5|97. Wondering what the significance of the creases is, the scholar hits on the step of adding the numbers created by them:


216 + 348 + 5 + 97 = 666

After that… Well, I haven’t written the story yet. But that beginning raises an obvious question. Is there any other way of getting a Number of the Creased from 216348597? That is, can you get 666, the Number of the Beast, by dividing 216348597 in another way? Yes, you can. In fact, there are six ways of creating 666 by dividing-and-summing 216348597:


666 = 2 + 1 + 634 + 8 + 5 + 9 + 7
666 = 2 + 163 + 485 + 9 + 7
666 = 216 + 348 + 5 + 97
666 = 21 + 63 + 485 + 97
666 = 21 + 6 + 34 + 8 + 597
666 = 2 + 16 + 3 + 48 + 597

216348597 is a permutation of 123456789, so does 123456789 yield a Number of the Creased? Yes. Two of them, in fact:


666 = 123 + 456 + 78 + 9
666 = 1 + 2 + 3 + 4 + 567 + 89

And 987654321 yields another:


666 = 9 + 87 + 6 + 543 + 21

And what about other permutations of 123456789? These are the successive records:

Using 123456789

666 = 123 + 456 + 78 + 9
666 = 1 + 2 + 3 + 4 + 567 + 89 (c=2)

Using 123564789

666 = 12 + 3 + 564 + 78 + 9
666 = 123 + 56 + 478 + 9
666 = 1 + 2 + 3 + 564 + 7 + 89 (c=3)

Using 125463978

666 = 1 + 2 + 5 + 4 + 639 + 7 + 8
666 = 12 + 546 + 3 + 97 + 8
666 = 1 + 254 + 6 + 397 + 8
666 = 1 + 2 + 546 + 39 + 78 (c=4)

Using 139462578

666 = 13 + 9 + 4 + 625 + 7 + 8
666 = 139 + 462 + 57 + 8
666 = 1 + 394 + 6 + 257 + 8
666 = 1 + 39 + 46 + 2 + 578
666 = 13 + 9 + 4 + 62 + 578 (c=5)

Using 216348597

666 = 2 + 1 + 634 + 8 + 5 + 9 + 7
666 = 2 + 163 + 485 + 9 + 7
666 = 216 + 348 + 5 + 97
666 = 21 + 63 + 485 + 97
666 = 21 + 6 + 34 + 8 + 597
666 = 2 + 16 + 3 + 48 + 597 (c=6)


216348597 is the best of the bestial. No other permutation of 123456789 yields as many as six Numbers of the Creased.

Sanctisonic Symmetry

by in Album Art, Art, Music and tagged , , , , , , , , , , | Leave a comment

Holy Fawn, Realms EP (2015)

I like the symmetry and simplicity of this cover, though I think the style and color of the text could be improved on. Here are two variants on the cover:

Cover without text

Cover with mirrored text

Elsewhere Other-Accessible…

• Holy Fawn at Bandcamp