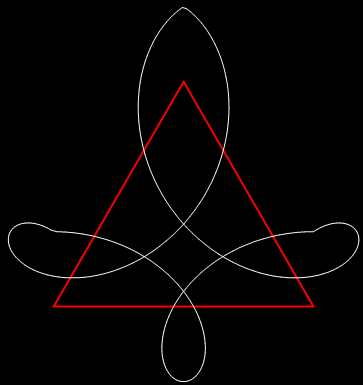
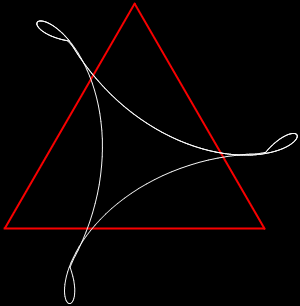
In his Penguin Dictionary of Curious and Interesting Numbers (1986), David Wells says that 142857 is “beloved of all recreational mathematicians”. He then says it’s the decimal period of the reciprocal of the fourth prime: “1/7 = 0·142857142857142…” And the reciprocal has maximum period. There are 6 = 7-1 digits before repetition begins, unlike the earlier prime reciprocals:
1/2 = 0·5
1/3 = 0·333...
1/5 = 0·2
1/7 = 0·142857 142857 142...
In other words, all possible remainders appear when you calculate the decimals of 1/7:
1*10 / 7 = 1 remainder 3 → 0·1
3*10 / 7 = 4 remainder 2 → 0·14
2*10 / 7 = 2 remainder 6 → 0·142
6*10 / 7 = 8 remainder 4 → 0·1428
4*10 / 7 = 5 remainder 5 → 0·14285
5*10 / 7 = 7 remainder 1 → 0·142857
1*10 / 7 = 1 remainder 3 → 0·142857 1
3*10 / 7 = 4 remainder 2 → 0·142857 14
2*10 / 7 = 2 remainder 6 → 0·142857 142...
That happens again with 1/17 and 1/19, but Wells says that “surprisingly, there is no known method of predicting which primes have maximum period.” It’s a simple question that involves some deep mathematics. Looking at prime reciprocals is like peering through a small window into a big room. Some things are easy to see, some are difficult and some are presently impossible.
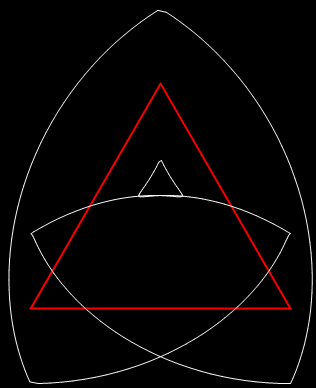
In his discussion of 142857, Wells mentions one way of peering through a period pane: “The sequence of digits also makes a striking pattern when the digits are arranged around a circle.” Here is the pattern, with ten points around the circle representing the digits 0 to 9:

The digits of 1/7 = 0·142857142…
But I prefer, for further peers through the period-panes, to create the period-panes using remainders rather than digits. That is, the number of points around the circle is determined by the prime itself rather than the base in which the reciprocal is calculated:

The remainders of 1/7 = 1, 3, 2, 6, 4, 5…
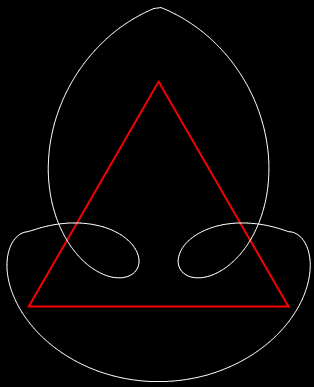
Period-panes can look like butterflies or bats or bivalves or spiders or crabs or even angels. Try the remainders of 1/13. This prime reciprocal doesn’t have maximum period: 1/13 = 0·076923 076923 076923… So there are only six remainders, creating this pattern:

remainders(1/13) = 1, 10, 9, 12, 3, 4
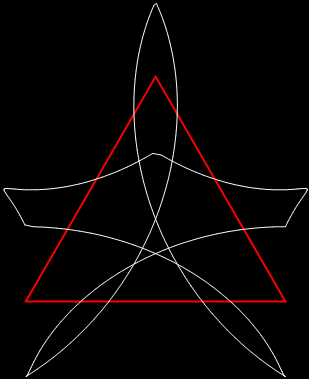
The multiple 2/13 has different remainders and creates a different pattern:

remainders(2/13) = 2, 7, 5, 11, 6, 8
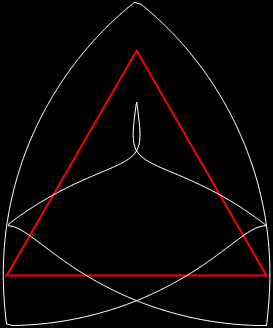
But 1/17, 1/19 and 1/23 all have maximum period and yield these period-panes:

remainders(1/17) = 1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12

remainders(1/19) = 1, 10, 5, 12, 6, 3, 11, 15, 17, 18, 9, 14, 7, 13, 16, 8, 4, 2

remainders(1/23) = 1, 10, 8, 11, 18, 19, 6, 14, 2, 20, 16, 22, 13, 15, 12, 5, 4, 17, 9, 21, 3, 7
It gets mixed again with the prime 73, which doesn’t have maximum period and yields a plethora of period-panes (some patterns repeat with different n * 1/73, so I haven’t included them):

remainders(1/73)

remainders(2/73)

remainders(3/73)

remainders(4/73)

remainders(5/73)

remainders(6/73)

remainders(9/73)

remainders(11/73) (identical to pattern of 5/73)

remainders(12/73)

remainders(18/73)
101 yields a plethora of period-panes, but they’re variations on a simple theme. They look like flapping wings in this animated gif:

remainders of n/101 (animated)
The remainders of 137 yield more complex period-panes:

remainders of n/137 (animated)
And what about different bases? Here are period-panes for the remainders of 1/17 in bases 2 to 16:

remainders(1/17) in base 2

remainders(1/17) in b3

remainders(1/17) in b4

remainders(1/17) in b5

remainders(1/17) in b6

remainders(1/17) in b7

remainders(1/17) in b8

remainders(1/17) in b9

remainders(1/17) in b10

remainders(1/17) in b11

remainders(1/17) in b12

remainders(1/17) in b13

remainders(1/17) in b14

remainders(1/17) in b15

remainders(1/17) in b16

remainders(1/17) in bases 2 to 16 (animated)
But the period-panes so far have given a false impression. They’ve all been symmetrical. That isn’t the case with all the period-panes of n/19:

remainders(1/19) in b2

remainders(1/19) in b3

remainders(1/19) in b4 = 1, 4, 16, 7, 9, 17, 11, 6, 5 (asymmetrical)

remainders(1/19) in b5 = 1, 5, 6, 11, 17, 9, 7, 16, 4 (identical pattern to that of b4)

remainders(1/19) in b6

remainders(1/19) in b7

remainders(1/19) in b8

remainders(1/19) in b9

remainders(1/19) in b10 (identical pattern to that of b2)

remainders(1/19) in b11

remainders(1/19) in b12

remainders(1/19) in b13

remainders(1/19) in b14

remainders(1/19) in b15

remainders(1/19) in b16

remainders(1/19) in b17

remainders(1/19) in b18

remainders(1/19) in bases 2 to 18 (animated)
Here are a few more period-panes in different bases:

remainders(1/11) in b2

remainders(1/11) in b7

remainders(1/13) in b6

remainders(1/43) in b6

remainders in b2 for reciprocals of 29, 37, 53, 59, 61, 67, 83, 101, 107, 131, 139, 149 (animated)
And finally, to performativize the pun of “period pane”, here are some period-panes for 1/29, whose maximum period will be 28 (NASA says that the “Moon takes about one month to orbit Earth … 27.3 days to complete a revolution, but 29.5 days to change from New Moon to New Moon”):

remainders(1/29) in b4

remainders(1/29) in b5

remainders(1/29) in b8

remainders(1/29) in b9

remainders(1/29) in b11

remainders(1/29) in b13

remainders(1/29) in b14

remainders(1/29) in various bases (animated)