Tag Archives: fractals

Blancmange Butterfly

by in Blancmange Curves, Circles, Fractals, Geometry, Mathematics and tagged , , , , , , , , , , , , , , , | Leave a comment

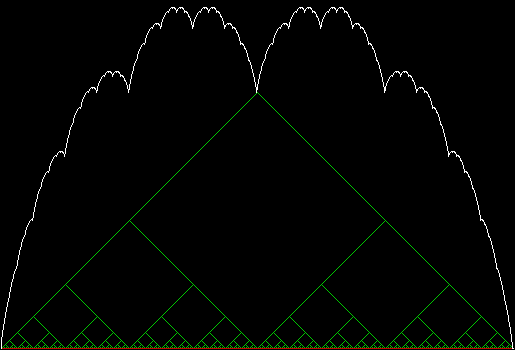
Blancmange butterfly. Is that a ’60s psychedelic band? No, it’s one of the shapes you can get by playing with blancmange curves. As I described in “White Rites”, a blancmange curve is a fractal created by summing the heights of successively smaller and more numerous zigzags, like this:

blanc_all

Zigzags 1 to 10

blancmange_all

Zigzags 1 to 10 (animated)

blanc_solid

Blancmange curve

In the blancmange curves below, the height (i.e., the y co-ordinate) has been normalized so that all the images are the same height:

Construction of a normalized blancmange curve (animated)

This is the solid version:

Solid normalized blancmange curve (animated)

I wondered what happens when you wrap a blancmange curve around a circle. Well, this happens:

Construction of a blancmange circle (animated)

You get what might be called a blancmange butterfly. The solid version looks like this (patterns in the circles are artefacts of the graphics program I used):

Solid blancmange circle (animated)

Next I tried using arcs rather zigzags to construct the blancmange curves and blancmange circles:

Arching blancmange curve (i.e., constructed with arcs) (animated)

And below is the circular version of a blancmange curve constructed with arcs. The arching circular blancmanges look even more like buttocks and then intestinal villi (the fingerlike projections lining our intestines):

Arching blancmange circle (animated)

The variations on blancmange curves don’t stop there — in fact, they’re infinite. Below is a negative arching blancmange curve, where the heights of the original arching blancmange curve are subtracted from the (normalized) maximum height:

Negative arching blancmange curve (animated)

And here’s an arching blancmange curve that’s alternately negative and positive:

Negative-positive arching blancmange curve (animated)

The circular version looks like this:

Negative-positive arching blancmange circle (animated)

Finally, here’s an arching blancmange curve that’s alternately positive and negative:

Positive-negative arching blancmange curve (animated)

And the circular version:

Positive-negative arching blancmange circle (animated)

Elsewhere Other-Accessible…

• White Rites — more variations on blancmange curves

Hour Power

by in Fractals, Geometry, Mathematics and tagged , , , | Leave a comment

How do you get an hourglass from this shape?

Rep-4 L-tromino

In fact, it’s easy. You simply divide the shape into four identical copies of itself, discard one copy, and repeat the process with each of the sub-copies:

l-triomino_124

Constructing an hourglass (animated)

↓

l-triomino_124_upright_static1

Hourglass (static)

Here are some more posts about what I call the hourglass fractal:

• The Hourglass Fractal at Overlord of the Über-feral

Extra Tetra

by in Fractals, Geometry, Mathematics and tagged , , , , , , , , , , , , | Leave a comment

Construction of a Sierpiński tetrahedron (from WikiMedia)

Post-Performative Post-Scriptum

The toxic title of this incendiary intervention radically references George Harrison’s album Extra Texture (1975).

Strange “S” in the Light

by in Fractals, Geometry, Mathematics and tagged , , , | Leave a comment

Unexpected discoveries are one of the joys of mathematics, even for amateurs. And computers help you make more of them, because computers make it easy to adjust variables or search faster and further through math-space than any unaided human ever could (on the downside, computers can make you lazy and blunt your intuition). Here’s an unexpected discovery I made using a computer in November 2020:

A distorted and dissected capital “S”

It’s a strange “S” that looks complex but is constructed very easily from three simple lines. And it’s a fractal, a shape that contains copies of itself at smaller and smaller scales:

Five sub-fractals of the Strange “S”

Elsewhere Other-Accessible…

• Fractangular Frolics — the Strange “S” in more light

We Can Circ It Out

by in Circles, Fractals, Geometry, Mathematics, Polygons, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

It’s a pretty little problem to convert this triangular fractal…

Sierpiński triangle (Wikipedia)

…into its circular equivalent:

Sierpiński triangle as circle

Sierpiński triangle to circle (animated)

But once you’ve circ’d it out, as it were, you can easily adapt the technique to fractals based on other polygons:

T-square fractal (Wikipedia)
⇓

T-square fractal as circle

T-square fractal to circle (animated)

Elsewhere other-accessible…

• Dilating the Delta — more on converting polygonic fractals to circles…

Fylfy Fractals

by in Fractals, Geometry, Mathematics, Rep-Tiles, Squares, Triangles and tagged , , , , , , , , , , | Leave a comment

An equilateral triangle is a rep-tile, because it can be tiled completely with smaller copies of itself. Here it is as a rep-4 rep-tile, tiled with four smaller copies of itself:

Equilateral triangle as rep-4 rep-tile

If you divide and discard one of the sub-copies, then carry on dividing-and-discarding with the sub-copies and sub-sub-copies and sub-sub-sub-copies, you get the fractal seen below. Alas, it’s not a very attractive or interesting fractal:

Divide-and-discard fractal stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Stage #9

Divide-and-discard fractal (animated)

You can create more attractive and interesting fractals by rotating the sub-triangles clockwise or anticlockwise. Here are some examples:

Now try dividing a square into four right triangles, then turning each of the four triangles into a divide-and-discard fractal. The resulting four-fractal shape is variously called a swastika, a gammadion, a cross cramponnée, a Hakenkreuz and a fylfot. I’m calling it a fylfy fractal:

Divide-and-discard fractals in the four triangles of a divided square stage #1

Fylfy fractal #2

Fylfy fractal #3

Fylfy fractal #4

Fylfy fractal #5

Fylfy fractal #6

Fylfy fractal #7

Fylfy fractal #8

Fylfy fractal (animated)

Finally, you can adjust the fylfy fractals so that each point in the square becomes the equivalent point in a circle:

Absolutely Sabulous

by in Fractals, Mathematics and tagged , , , , , , , , , | Leave a comment

The Hourglass Fractal (animated gif optimized at ezGIF)

Performativizing Paronomasticity

The title of this incendiary intervention is a paronomasia on the title of the dire Absolutely Fabulous. The adjective sabulous means “sandy; consisting of or abounding in sand; arenaceous” (OED).

Elsewhere Other-Accessible

• Hour Re-Re-Re-Re-Powered — more on the hourglass fractal
• Allus Pour, Horic — an earlier paronomasia for the fractal

Game of Throwns

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , | Leave a comment

In “Scaffscapes”, I looked at these three fractals and described how they were in a sense the same fractal, even though they looked very different:

Fractal #1

Fractal #2

Fractal #3

But even if they are all the same in some mathematical sense, their different appearances matter in an aesthetic sense. Fractal #1 is unattractive and seems uninteresting:

Fractal #1, unattractive, uninteresting and unnamed

Fractal #3 is attractive and interesting. That’s part of why mathematicians have given it a name, the T-square fractal:

Fractal #3 — the T-square fractal

But fractal #2, although it’s attractive and interesting, doesn’t have a name. It reminds me of a ninja throwing-star or shuriken, so I’ve decided to call it the throwing-star fractal or ninja-star fractal:

Fractal #2, the throwing-star fractal

A ninja throwing-star or shuriken

This is one way to construct a throwing-star fractal:

Throwing-star fractal, stage 1

Throwing-star fractal, #2

Throwing-star fractal, #3

Throwing-star fractal, #4

Throwing-star fractal, #5

Throwing-star fractal, #6

Throwing-star fractal, #7

Throwing-star fractal, #8

Throwing-star fractal, #9

Throwing-star fractal, #10

Throwing-star fractal, #11

Throwing-star fractal (animated)

But there’s another way to construct a throwing-star fractal. You use what’s called the chaos game. To understand the commonest form of the chaos game, imagine a ninja inside an equilateral triangle throwing a shuriken again and again halfway towards a randomly chosen vertex of the triangle. If you mark each point where the shuriken lands, you eventually get a fractal called the Sierpiński triangle:

Chaos game with triangle stage 1

Chaos triangle #2

Chaos triangle #3

Chaos triangle #4

Chaos triangle #5

Chaos triangle #6

Chaos triangle #7

Chaos triangle (animated)

When you try the chaos game with a square, with the ninja throwing the shuriken again and again halfway towards a randomly chosen vertex, you don’t get a fractal. The interior of the square just fills more or less evenly with points:

Chaos game with square, stage 1

Chaos square #2

Chaos square #3

Chaos square #4

Chaos square #5

Chaos square #6

Chaos square (anim)

But suppose you restrict the ninja’s throws in some way. If he can’t throw twice or more in a row towards the same vertex, you get a familiar fractal:

Chaos game with square, ban on throwing towards same vertex, stage 1

Chaos square, ban = v+0, #2

Chaos square, ban = v+0, #3

Chaos square, ban = v+0, #4

Chaos square, ban = v+0, #5

Chaos square, ban = v+0, #6

Chaos square, ban = v+0 (anim)

But what if the ninja can’t throw the shuriken towards the vertex one place anti-clockwise of the vertex he’s just thrown it towards? Then you get another familiar fractal — the throwing-star fractal:

Chaos square, ban = v+1, stage 1

Chaos square, ban = v+1, #2

Chaos square, ban = v+1, #3

Chaos square, ban = v+1, #4

Chaos square, ban = v+1, #5

Game of Throwns — throwing-star fractal from chaos game (static)

Game of Throwns — throwing-star fractal from chaos game (anim)

And what if the ninja can’t throw towards the vertex two places anti-clockwise (or two places clockwise) of the vertex he’s just thrown the shuriken towards? Then you get a third familiar fractal — the T-square fractal:

Chaos square, ban = v+2, stage 1

Chaos square, ban = v+2, #2

Chaos square, ban = v+2, #3

Chaos square, ban = v+2, #4

Chaos square, ban = v+2, #5

T-square fractal from chaos game (static)

T-square fractal from chaos game (anim)

Finally, what if the ninja can’t throw towards the vertex three places anti-clockwise, or one place clockwise, of the vertex he’s just thrown the shuriken towards? If you can guess what happens, your mathematical intuition is much better than mine.

Post-Performative Post-Scriptum

I am not now and never have been a fan of George R.R. Martin. He may be a good author but I’ve always suspected otherwise, so I’ve never read any of his books or seen any of the TV adaptations.