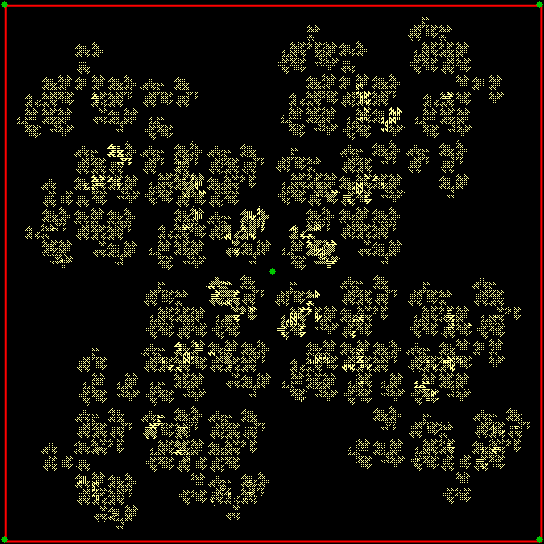Suppose you start at the middle of a triangle, then map all possible ways you can jump eight times half-way towards one or another of the vertices of the triangle. At the end of the eight jumps, you mark your final position with a dot. You could jump eight times towards the same vertex, or once towards vertex 1, once towards vertex 2, and once again towards vertex 1. And so on. If you do this, the record of your jumps looks something like this:

The shape is a fractal called the Sierpiński triangle. But if you try the same thing with a square — map all possible jumping-routes you can follow towards one or another of the four vertices — you simply fill the interior of the square. There’s no interesting fractal:

So you need a plan with a ban. Try mapping all possible routes where you can’t jump towards the same vertex twice in a row. And you get this:

Ban on jumping towards same vertex twice in a row, v(t) ≠ v(t-1)
If you call the current vertex v(t) and the previous vertex v(t-1), the ban says that v(t) ≠ v(t-1). Now suppose you can’t jump towards the vertex one place clockwise of the previous vertex. Now the ban is v(t)-1 ≠ v(t-1) or v(t) ≠ v(t-1)+1 and this fractal appears:
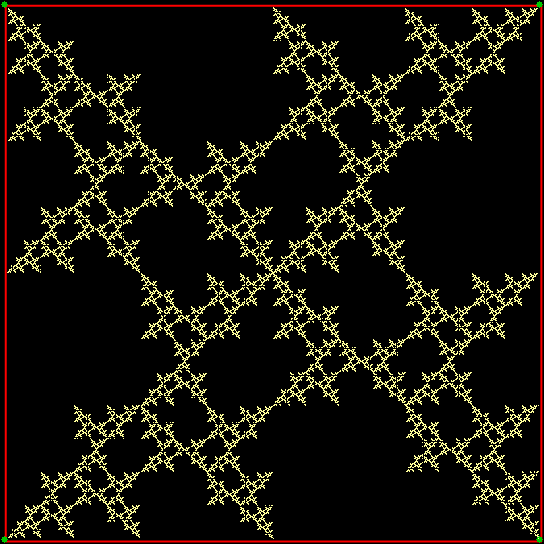
v(t) ≠ v(t-1)+1
And here’s a ban on jumping towards the vertex two places clockwise (or counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+2
And finally the ban on jumping towards the vertex three places clockwise (or one place counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+3 (a mirror-image of v(t) ≠ v(t-1)+1, as above)
Now suppose you introduce a new point to jump towards at the middle of the square. You can create more fractals, but you have to adjust the kind of ban you use. The central point can’t be included in the ban or the fractal will be asymmetrical. So you continue taking account of the vertices, but if the previous jump was towards the middle, you ignore that jump. At least, that’s what I intended, but I wonder whether my program works right. Anyway, here are some of the fractals that it produces:
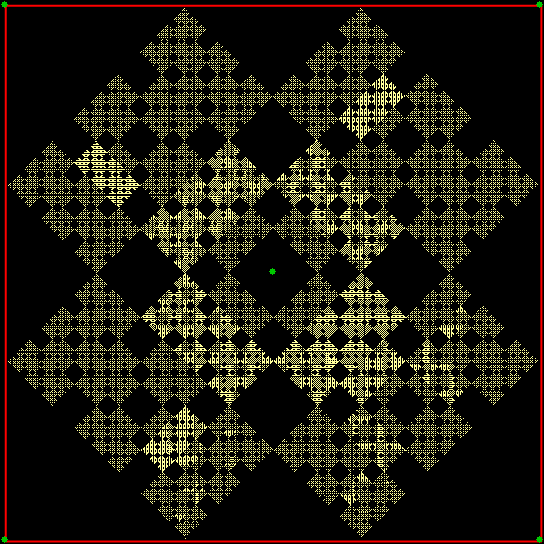
v(t) ≠ v(t-1) with central point (wcp)

v(t) ≠ v(t-1)+1, wcp

v(t) ≠ v(t-1)+2, wcp
And here are some bans taking account of both the previous vertex and the pre-previous vertex:
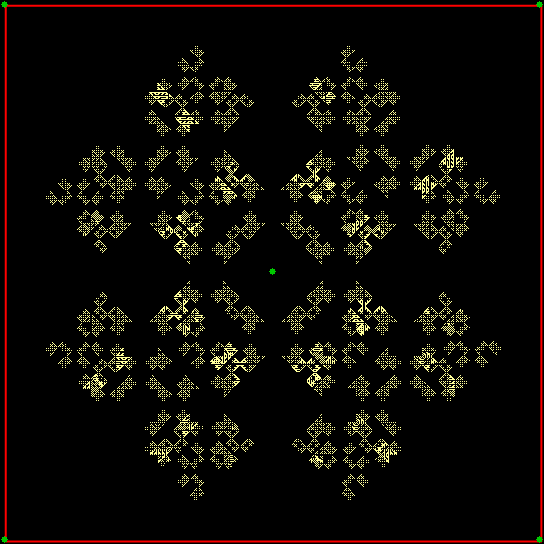
v(t) ≠ v(t-1) & v(t) ≠ v(t-2), wcp
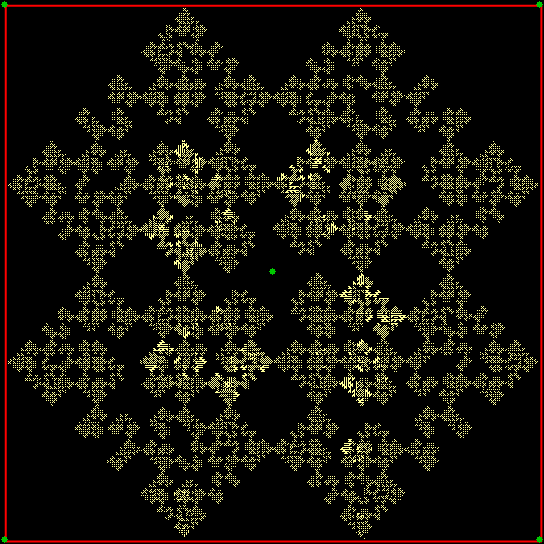
v(t) ≠ v(t-1) & v(t-2)+1, wcp
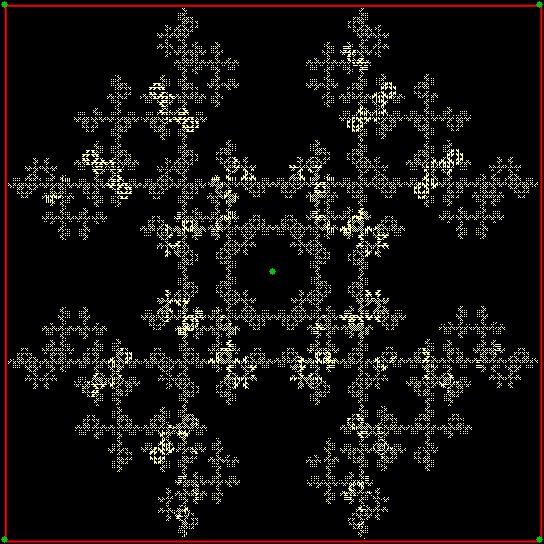
v(t) ≠ v(t-1)+2 & v(t-2), wcp
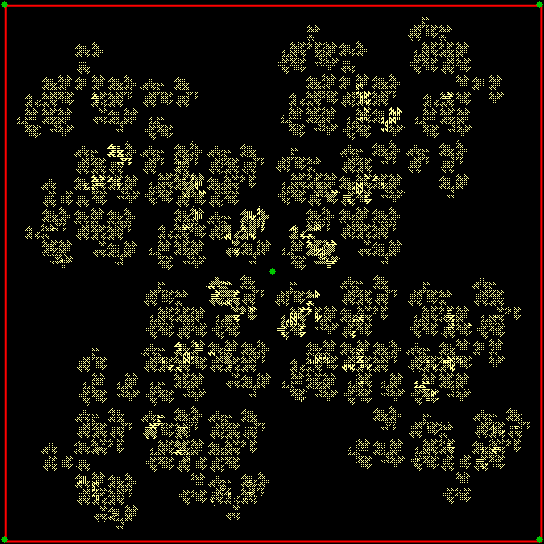
v(t) ≠ v(t-1) & v(t-2)+1, wcp
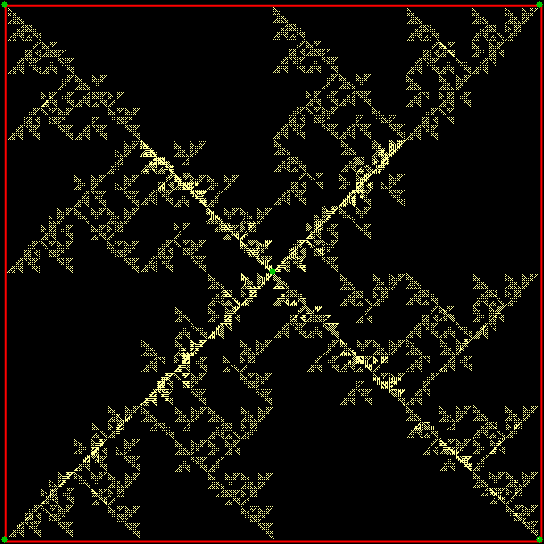
v(t) ≠ v(t-1)+1 & v(t-2)+1, wcp
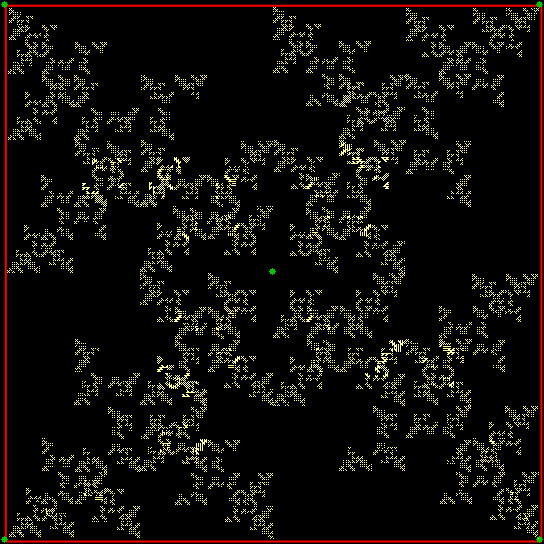
v(t) ≠ v(t-1)+2 & v(t-2)+1, wcp
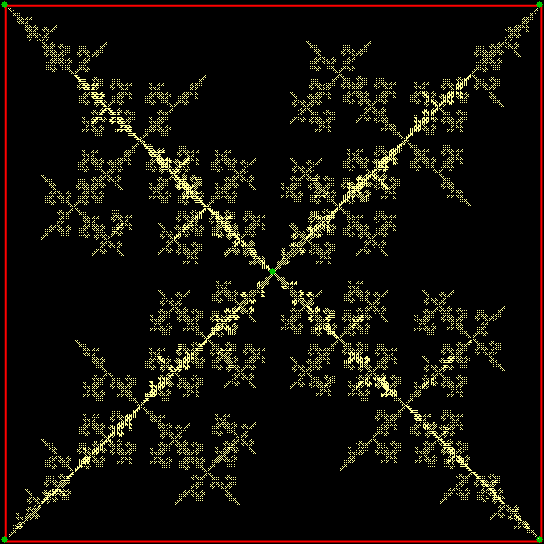
v(t) ≠ v(t-1)+3 & v(t-2)+1, wcp
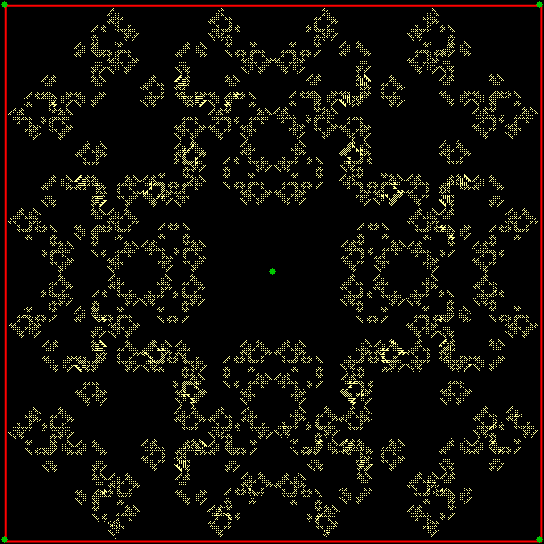
v(t) ≠ v(t-1) & v(t-2)+2, wcp
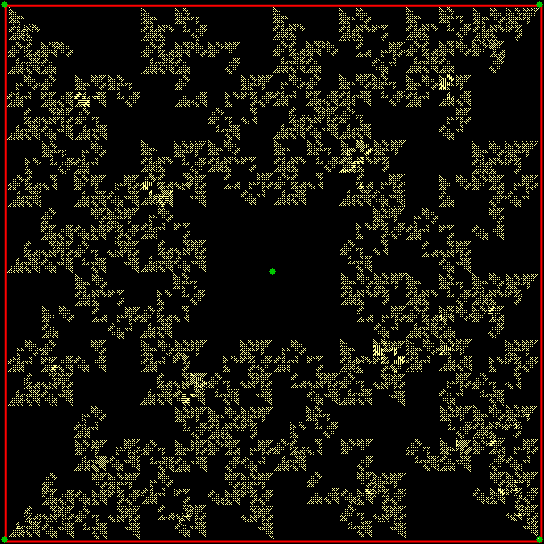
v(t) ≠ v(t-1)+1 & v(t-2)+2, wcp

v(t) ≠ v(t-1)+2 & v(t-2)+2, wcp
Now look at pentagons. They behave more like triangles than squares when you map all possible jumping-routes towards one or another of the five vertices. That is, a fractal appears:

All possible jumping-routes towards the vertices of a pentagon
But the pentagonal-jump fractals get more interesting when you introduce jump-bans:

v(t) ≠ v(t-1)

v(t) ≠ v(t-1)+1

v(t) ≠ v(t-1)+2

v(t) ≠ v(t-1) & v(t-2)

v(t) ≠ v(t-1)+2 & v(t-2)

v(t) ≠ v(t-1)+1 & v(t-2)+1

v(t) ≠ v(t-1)+3 & v(t-2)+1

v(t) ≠ v(t-1)+1 & v(t-2)+2

v(t) ≠ v(t-1)+2 & v(t-2)+2

v(t) ≠ v(t-1)+3 & v(t-2)+2
Finally, here are some pentagonal-jump fractals using a central point:







Post-Performative Post-Scriptum
I’m not sure if I’ve got the order of some bans right above. For example, should v(t) ≠ v(t-1)+1 & v(t-2)+2 really be v(t) ≠ v(t-1)+2 & v(t-2)+1? I don’t know and I’m not going to check. But the idea of jumping-point bans is there and that’s all you need if you want to experiment with these fractal methods for yourself.