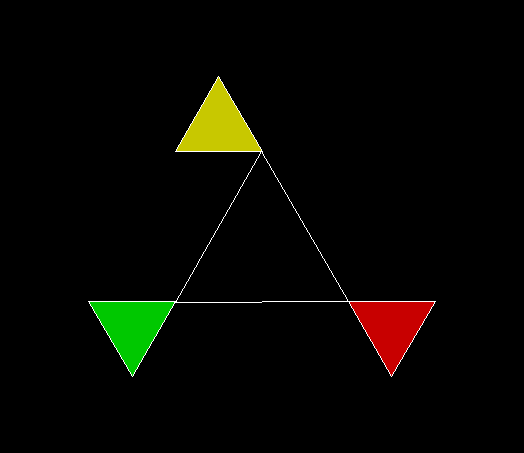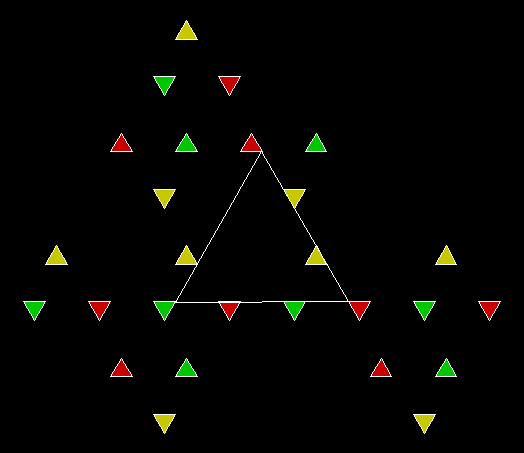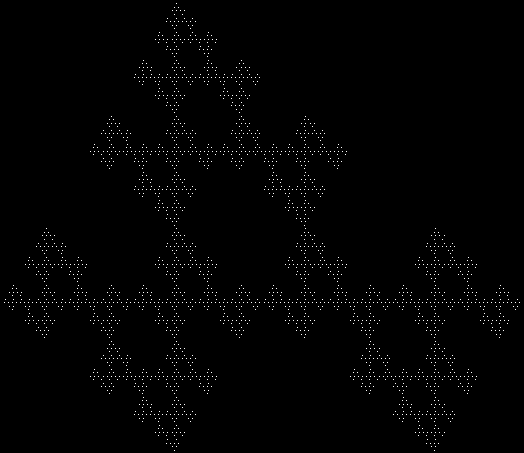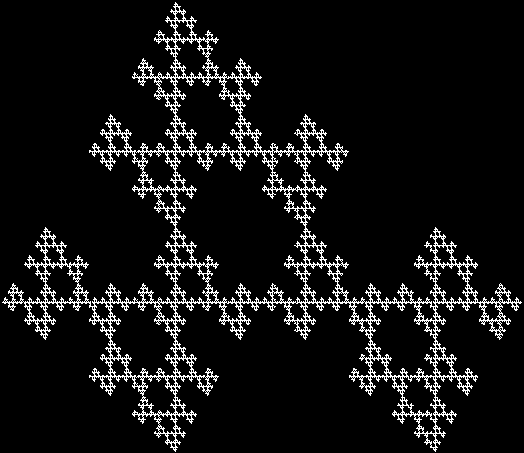
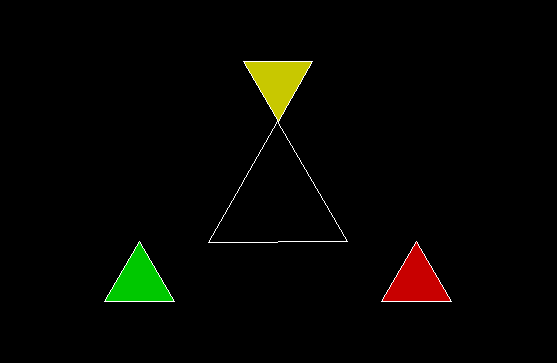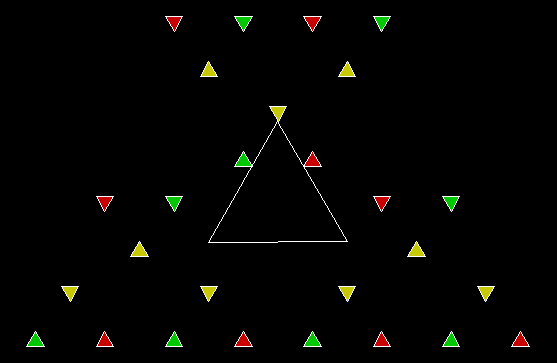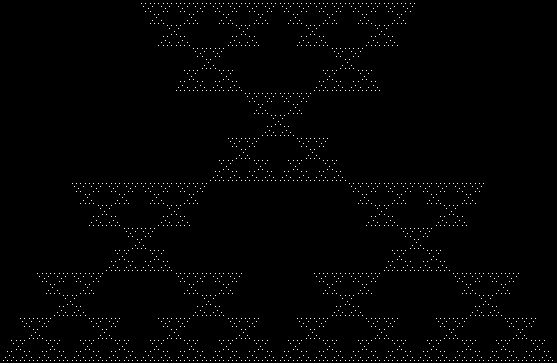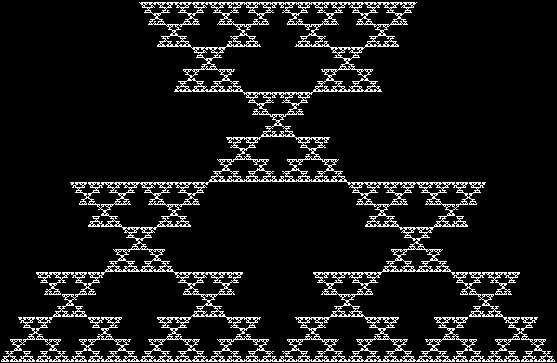
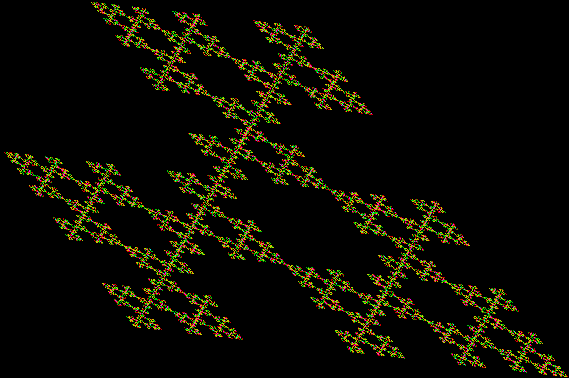
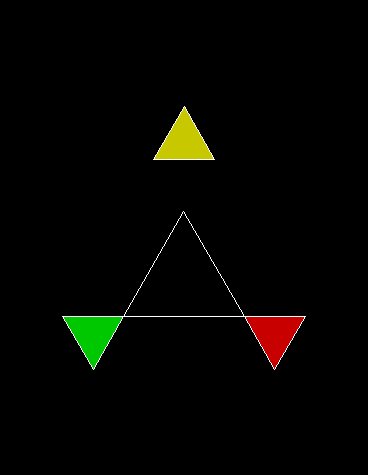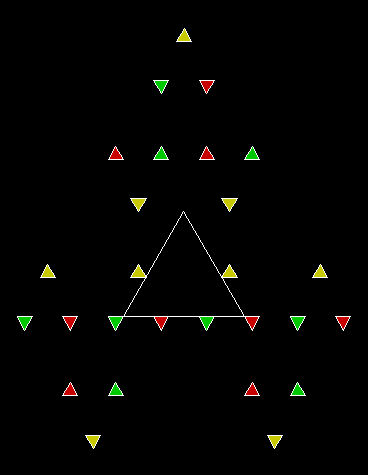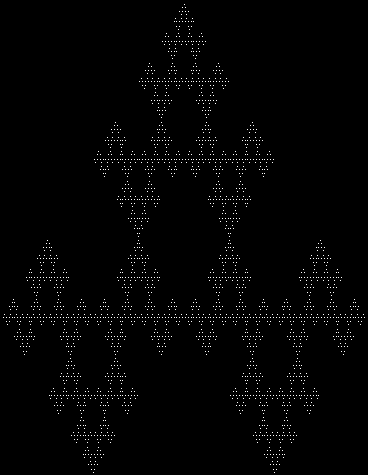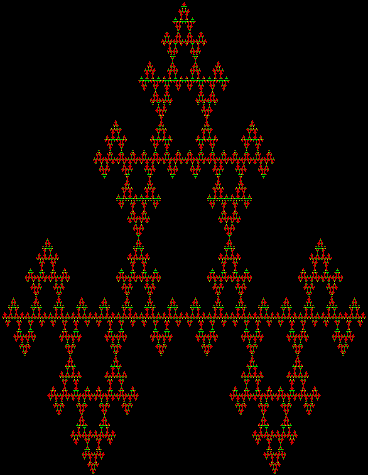
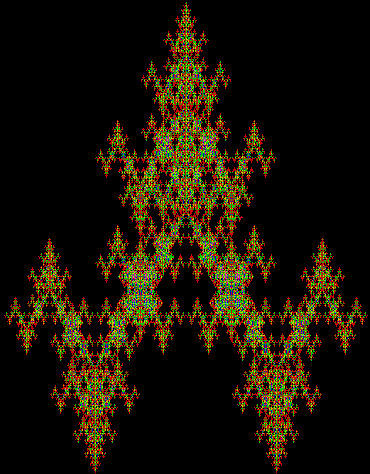
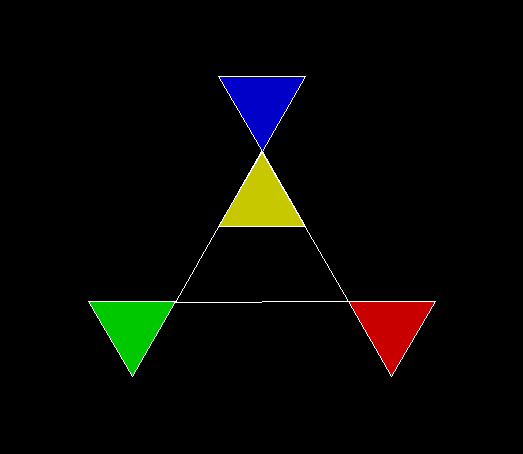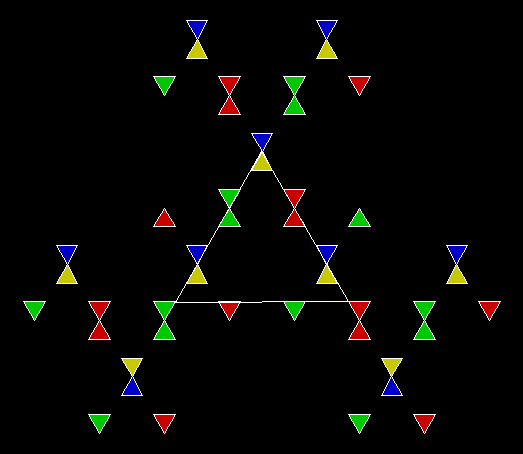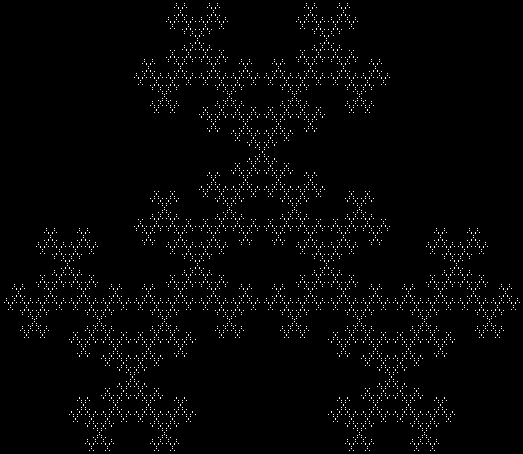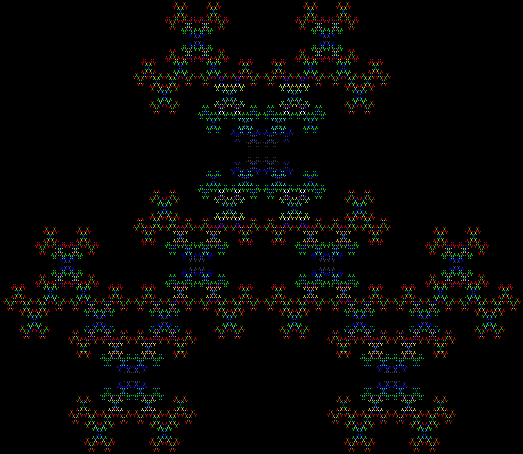
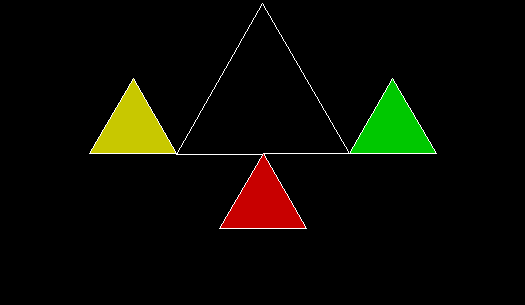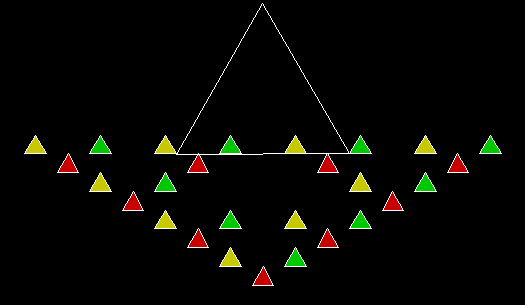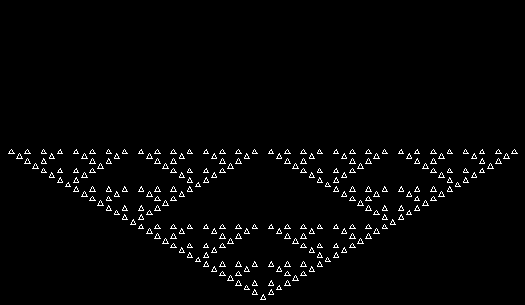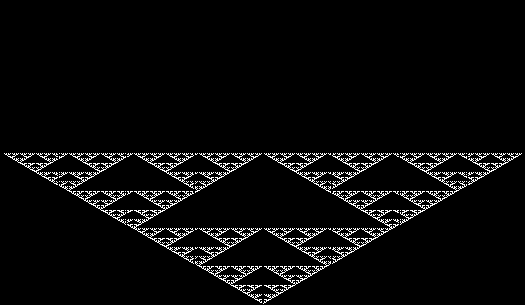
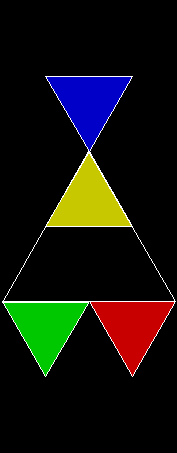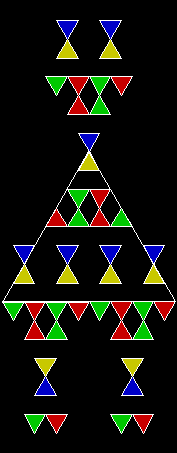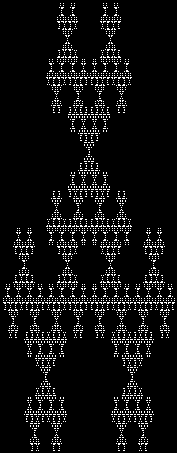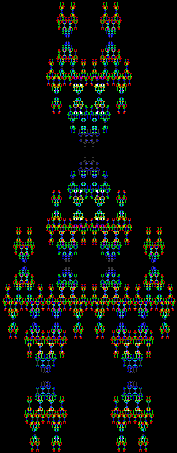
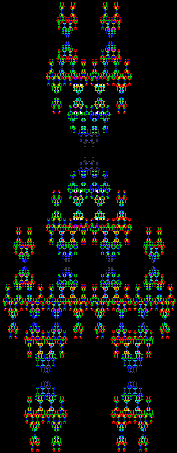
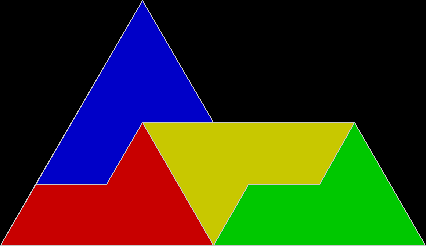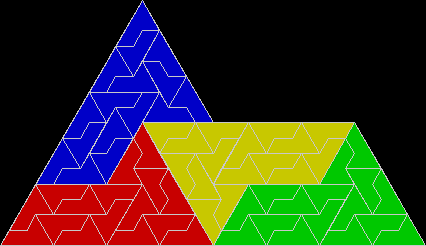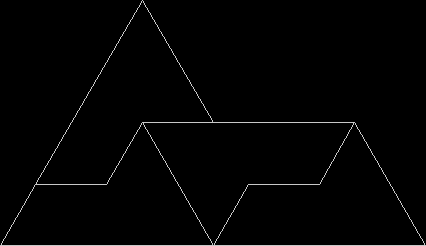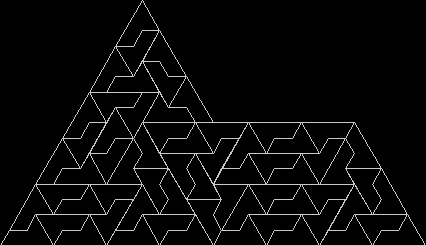
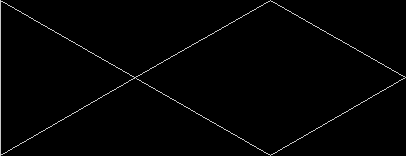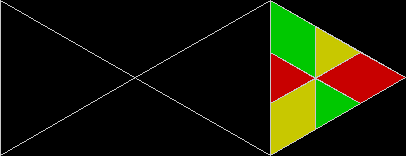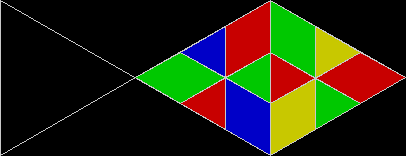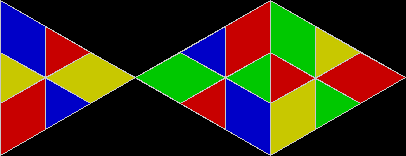
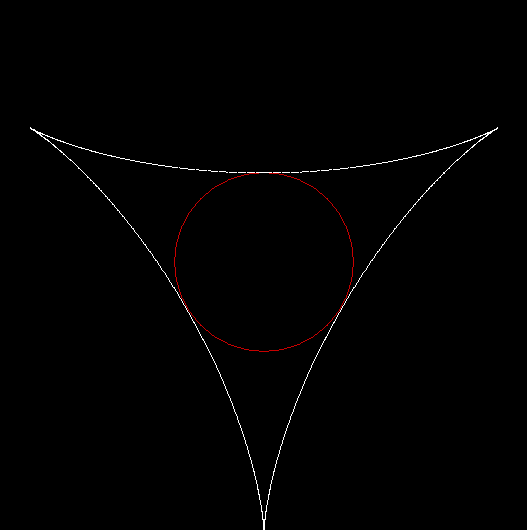
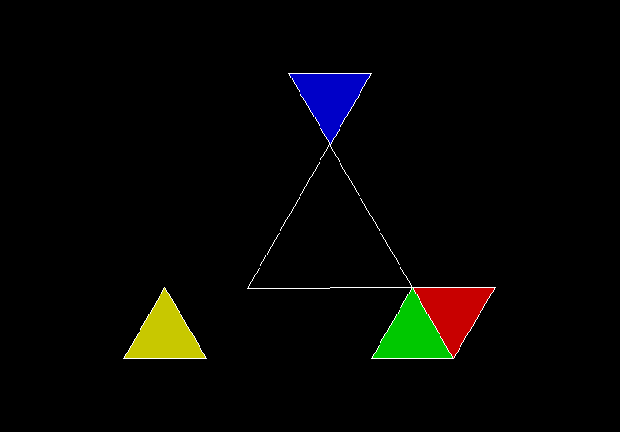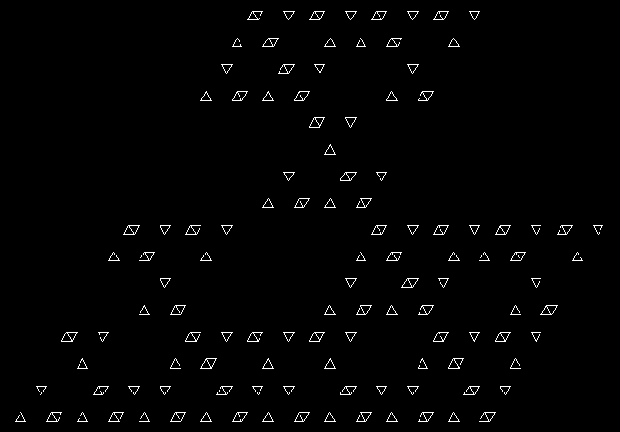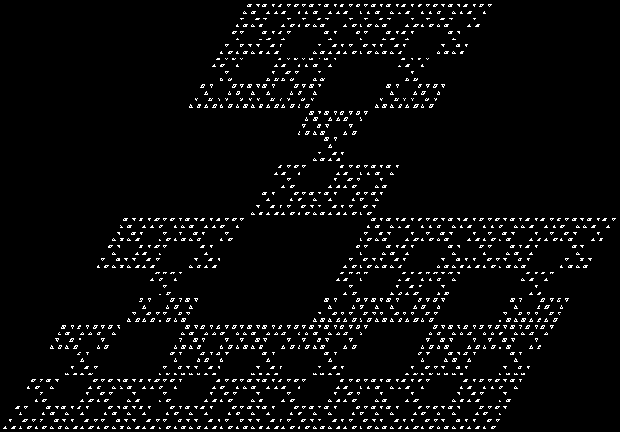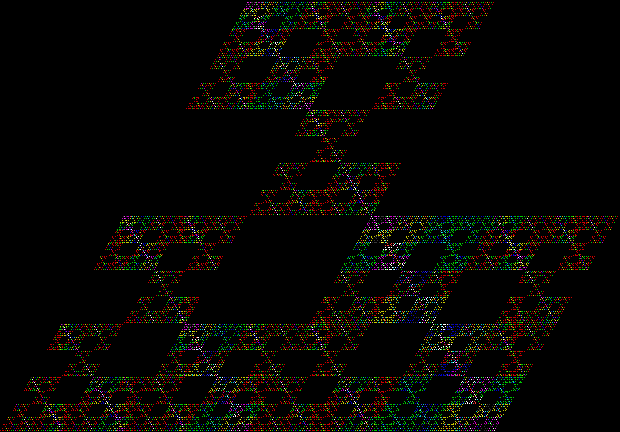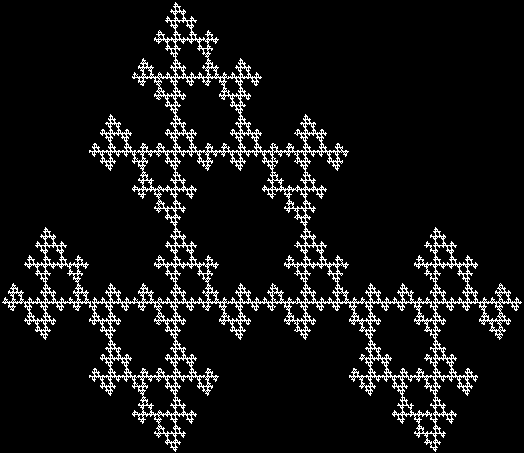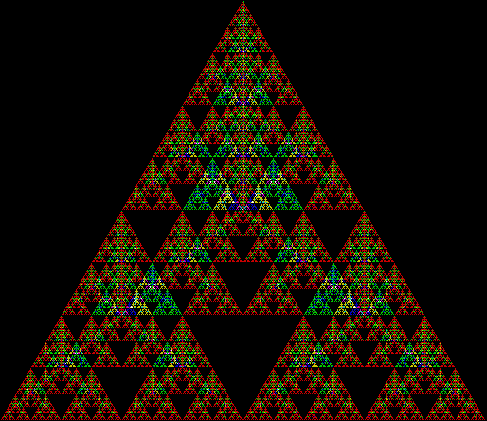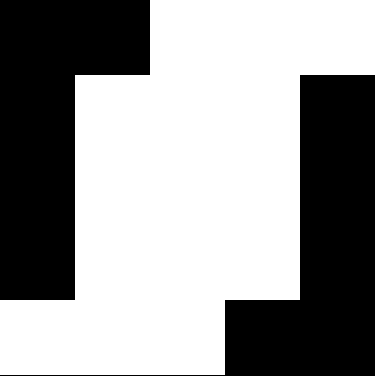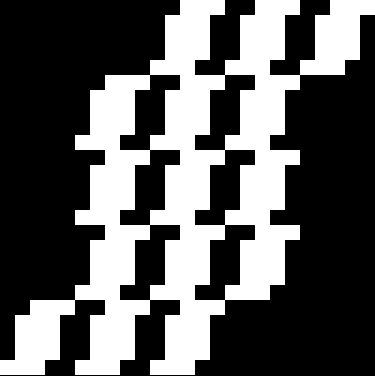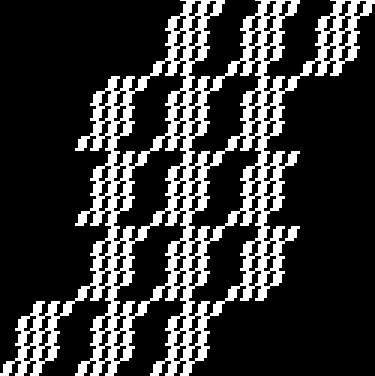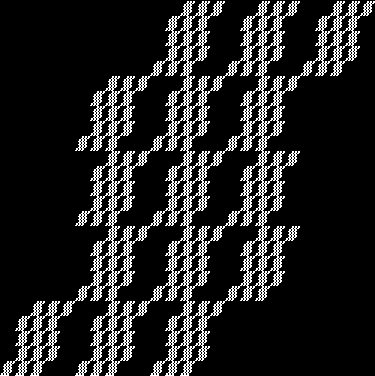In Boldly Breaking the Boundaries, I looked at the use of squares in what I called over-fractals, or fractals whose sub-divisions reproduce the original shape but appear beyond its boundaries. Now I want to look at over-fractals using triangles. They’re less varied than those involving squares, but still include some interesting shapes. This is the space in which sub-triangles can appear, with the central seeding triangle coloured gray: 
Here are some over-fractals based on the pattern above: 
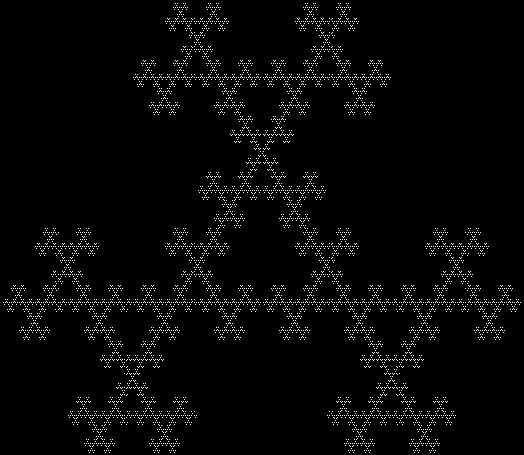
Tag Archives: geometry
Boldly Breaking the Boundaries
In “M.I.P. Trip”, I looked at fractals like this, in which a square is divided repeatedly into a pattern of smaller squares:

As you can see, the sub-squares appear within the bounds of the original square. But what if some of the sub-squares appear beyond the bounds of the original square? Then a new family of fractals is born, the over-fractals:
Lette’s Roll
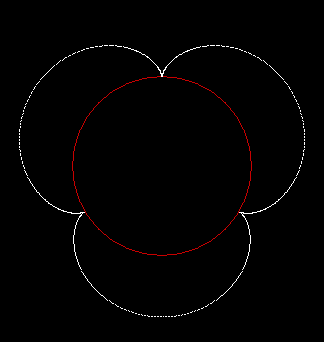
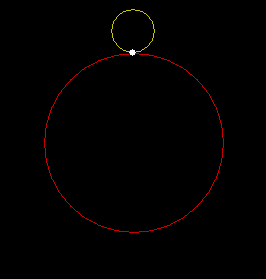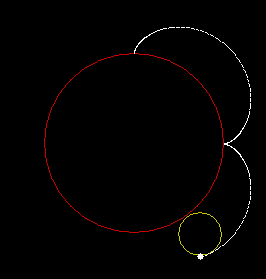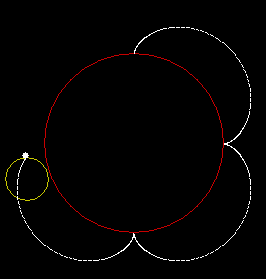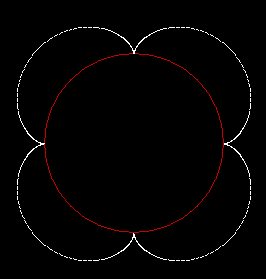
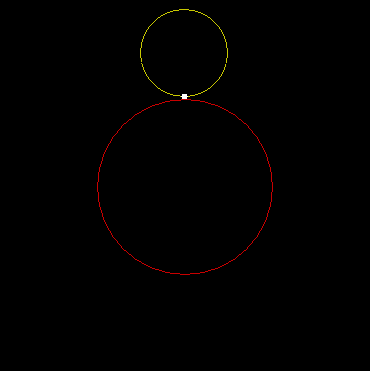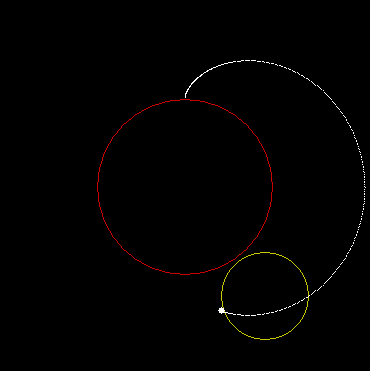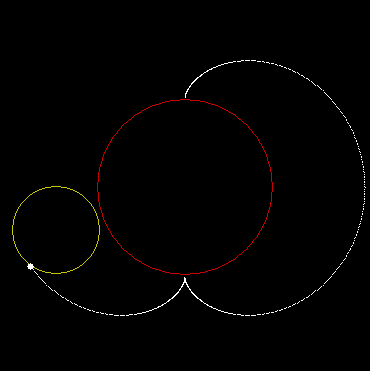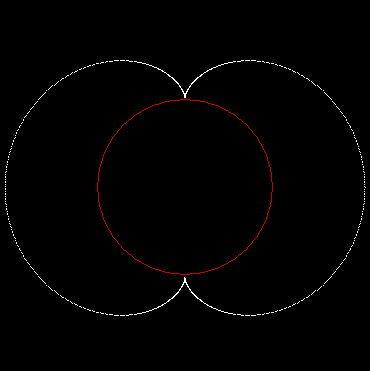
A roulette is a little wheel or little roller, but it’s much more than a game in a casino. It can also be one of a family of curves created by tracing the path of a point on a rotating circle. Suppose a circle rolls around another circle of the same size. This is the resultant roulette:


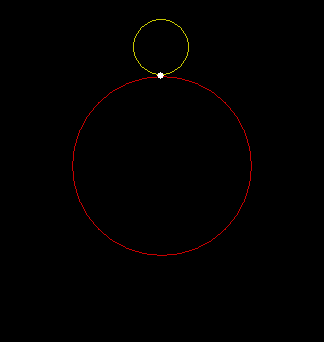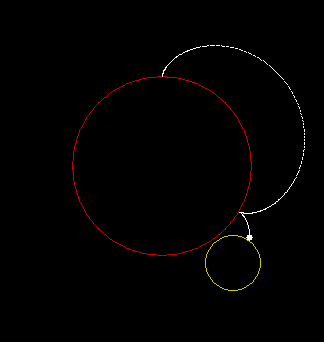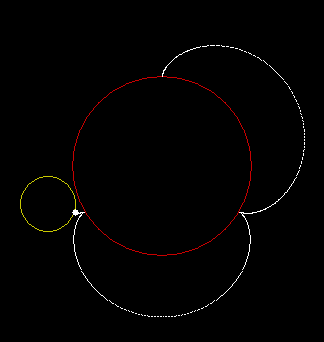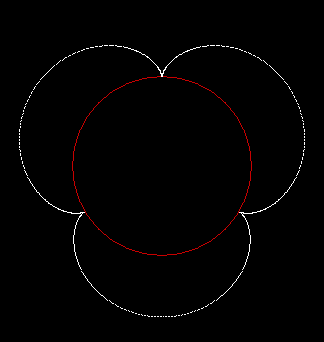
The shape is called a cardioid, because it looks like a heart (kardia in Greek). Now here’s a circle with radius r rolling around a circle with radius 2r:
That shape is a nephroid, because it looks like a kidney (nephros in Greek).
This is a circle with radius r rolling around a circle with radius 3r:

The shapes above might be called outer roulettes. But what if a circle rolls inside another circle? Here’s an inner roulette whose radius is three-fifths (0.6) x the radius of its rollee:


The same roulette appears inverted when the inner circle has a radius two-fifths (0.4) x the radius of the rollee:

But what happens when the circle rolling “inside” is larger than the rollee? That is, when the rolling circle is effectively swinging around the rollee, like a bunch of keys being twirled on an index finger? If the rolling radius is 1.5 times larger, the roulette looks like this:

If the rolling radius is 2 times larger, the roulette looks like this:
Here are more outer, inner and over-sized roulettes:
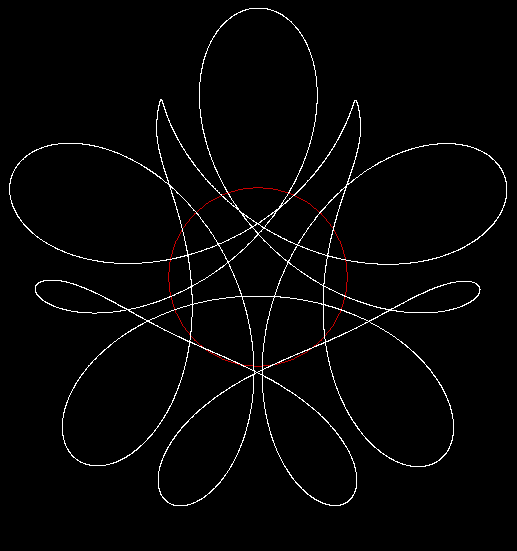
And you can have circles rolling inside circles inside circles:
And here’s another circle-in-a-circle in a circle:
M.i.P. Trip
The Latin phrase multum in parvo means “much in little”. It’s a good way of describing the construction of fractals, where the application of very simple rules can produce great complexity and beauty. For example, what could be simpler than dividing a square into smaller squares and discarding some of the smaller squares?
Yet repeated applications of divide-and-discard can produce complexity out of even a 2×2 square. Divide a square into four squares, discard one of the squares, then repeat with the smaller squares, like this:
Increase the sides of the square by a little and you increase the number of fractals by a lot. A 3×3 square yields these fractals:
And the 4×4 and 5×5 fractals yield more:

The Hex Fractor
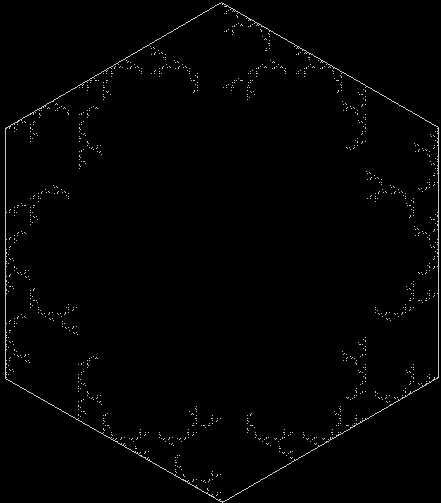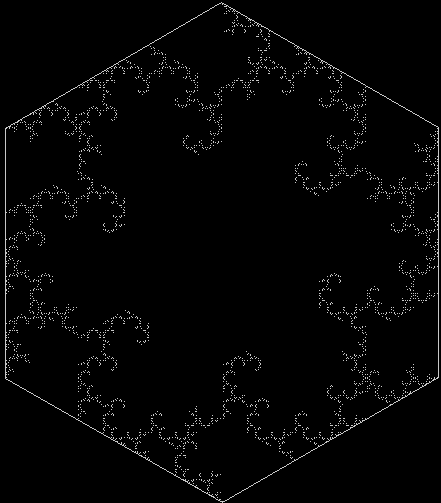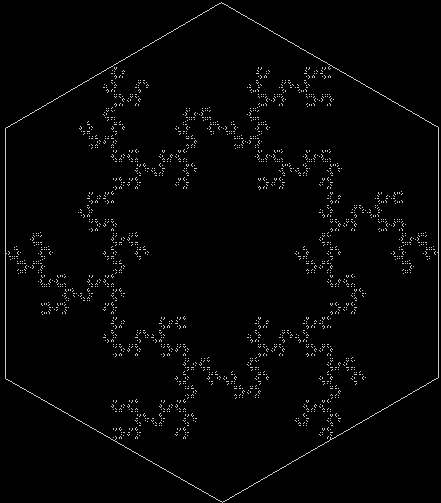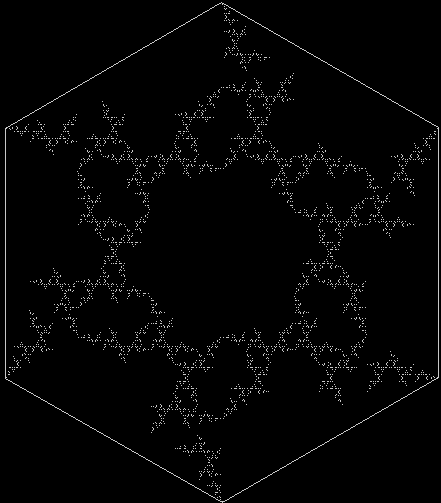
A regular hexagon can be divided into six equilateral triangles. An equilateral triangle can be divided into three more equilateral triangles and a regular hexagon. If you discard the three triangles and repeat, you create a fractal, like this:

Adjusting the sides of the internal hexagon creates new fractals:


Discarding a hexagon after each subdivision creates new shapes:



And you can start with another regular polygon, divide it into triangles, then proceed with the hexagons:

Sphaerocephalus

Echinops sphaerocephalus, or Great Globe Thistle
Hex Appeal
A polyiamond is a shape consisting of equilateral triangles joined edge-to-edge. There is one moniamond, consisting of one equilateral triangle, and one diamond, consisting of two. After that, there are one triamond, three tetriamonds, four pentiamonds and twelve hexiamonds. The most famous hexiamond is known as the sphinx, because it’s reminiscent of the Great Sphinx of Giza:
It’s famous because it is the only known pentagonal rep-tile, or shape that can be divided completely into smaller copies of itself. You can divide a sphinx into either four copies of itself or nine copies, like this (please open images in a new window if they fail to animate):
So far, no other pentagonal rep-tile has been discovered. Unless you count this double-triangle as a pentagon:
It has five sides, five vertices and is divisible into sixteen copies of itself. But one of the vertices sits on one of the sides, so it’s not a normal pentagon. Some might argue that this vertex divides the side into two, making the shape a hexagon. I would appeal to these ancient definitions: a point is “that which has no part” and a line is “a length without breadth” (see Neuclid on the Block). The vertex is a partless point on the breadthless line of the side, which isn’t altered by it.
But, unlike the sphinx, the double-triangle has two internal areas, not one. It can be completely drawn with five continuous lines uniting five unique points, but it definitely isn’t a normal pentagon. Even less normal are two more rep-tiles that can be drawn with five continuous lines uniting five unique points: the fish that can be created from three equilateral triangles and the fish that can be created from four isosceles right triangles:
Rep It Up
When I started to look at rep-tiles, or shapes that can be divided completely into smaller copies of themselves, I wanted to find some of my own. It turns out that it’s easy to automate a search for the simpler kinds, like those based on equilateral triangles and right triangles.
(Please open the following images in a new window if they fail to animate)
Previously pre-posted (please peruse):
Hextra Texture
A hexagon can be divided into six equilateral triangles. An equilateral triangle can be divided into a hexagon and three more equilateral triangles. These simple rules, applied again and again, can be used to create fractals, or shapes that echo themselves on smaller and smaller scales.
Previously pre-posted (please peruse):