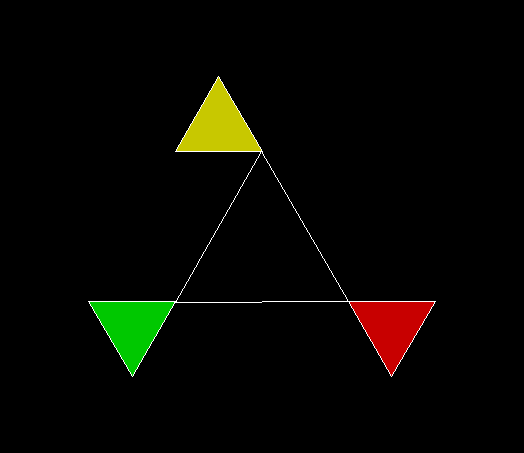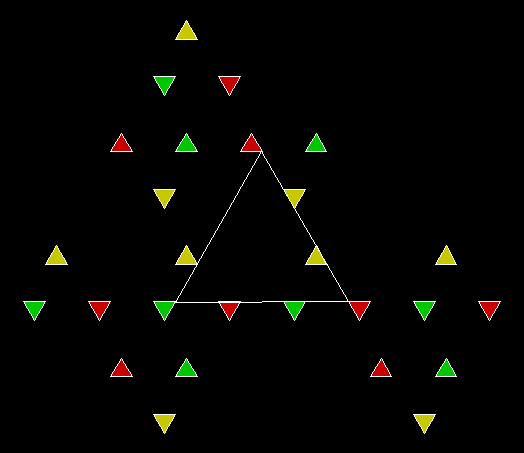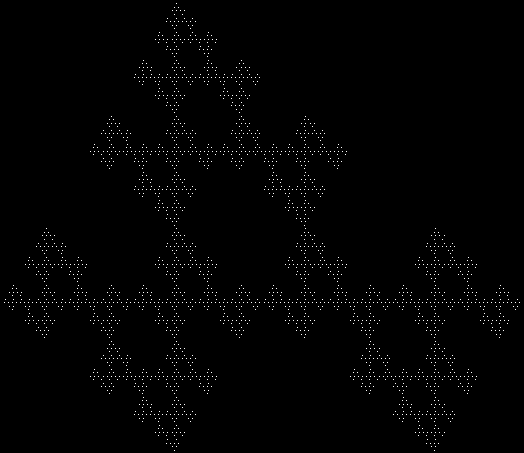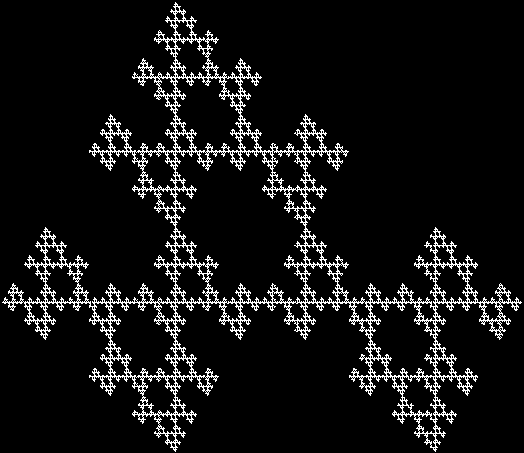
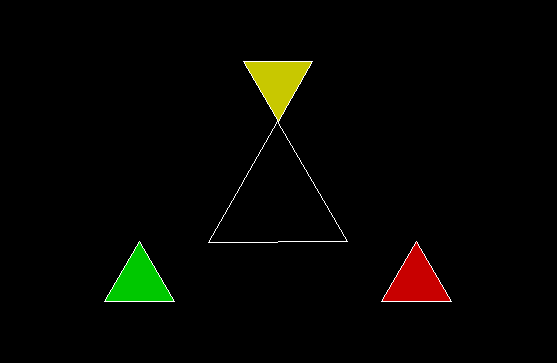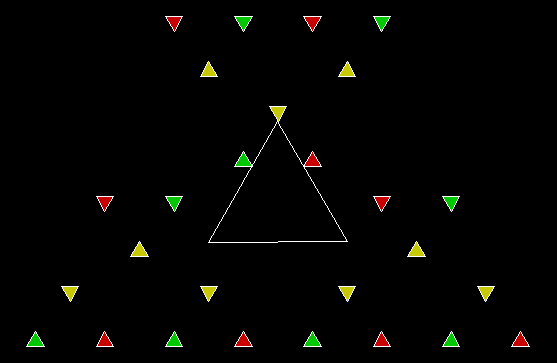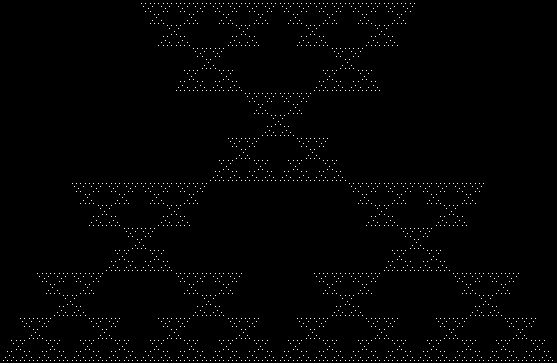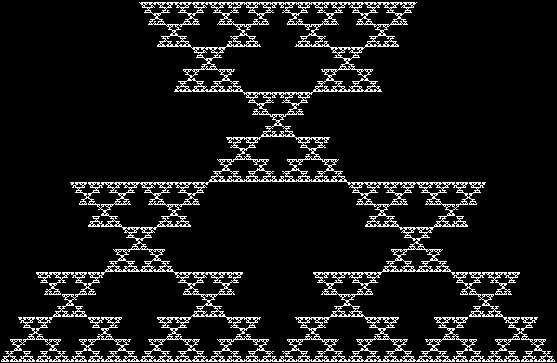
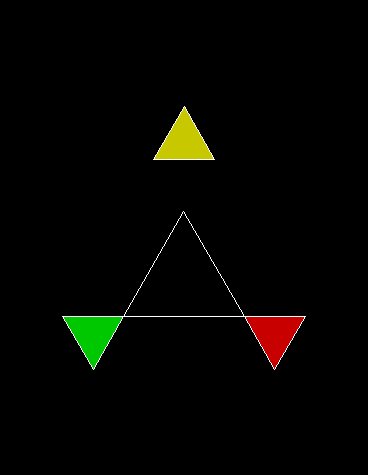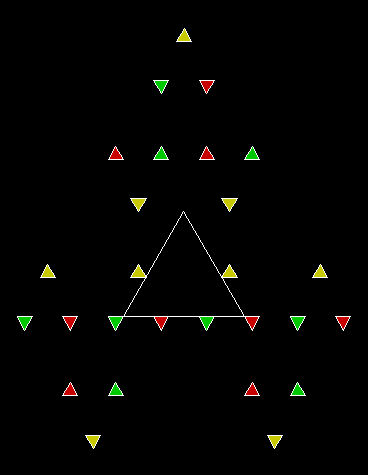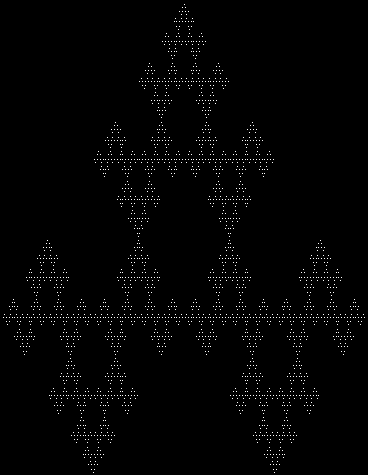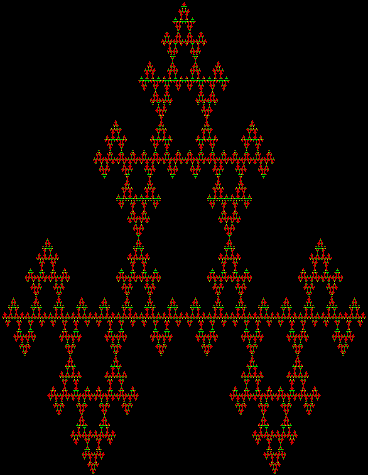
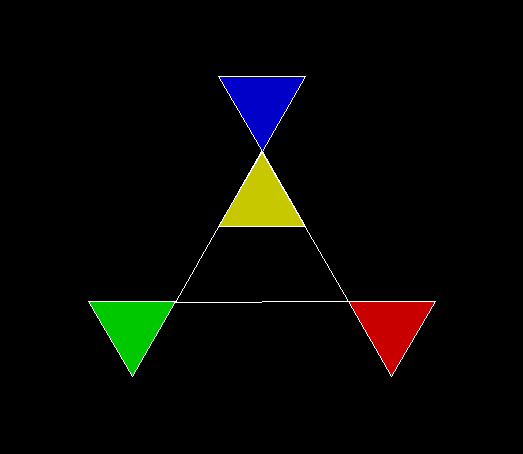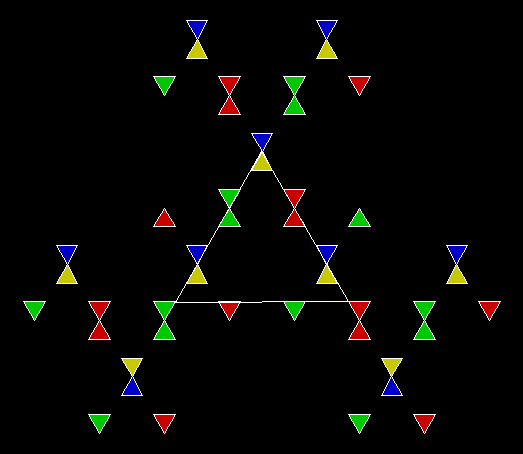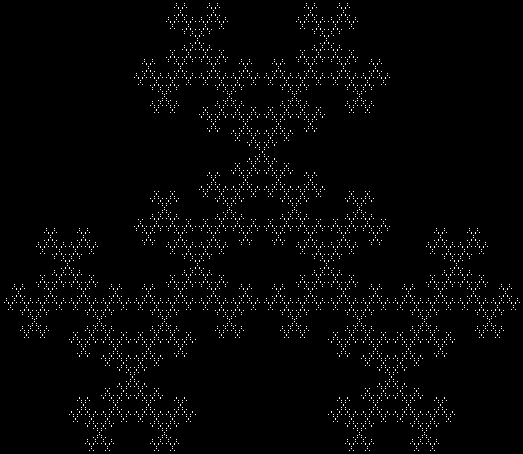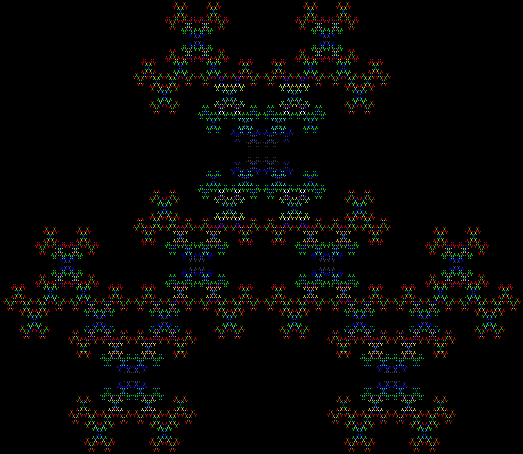
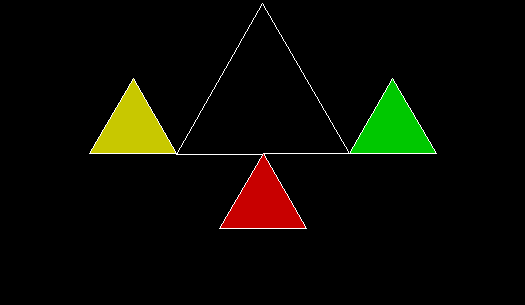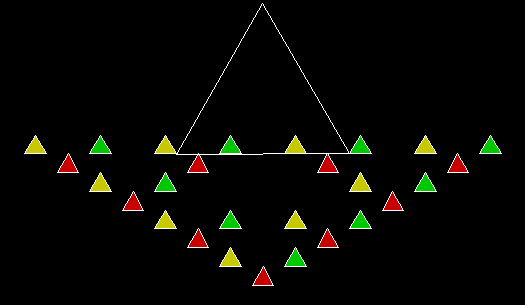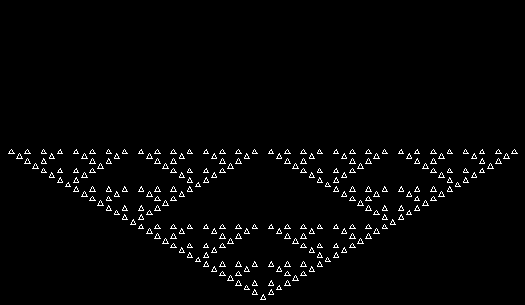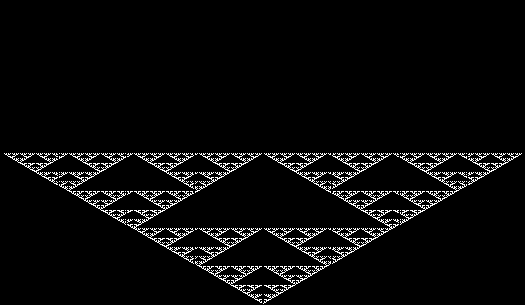
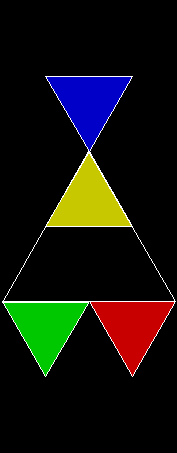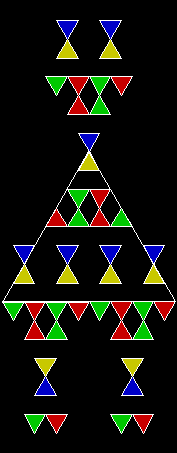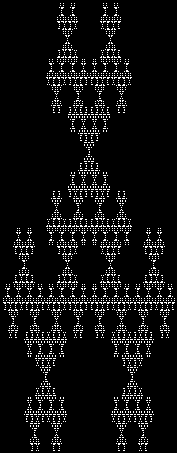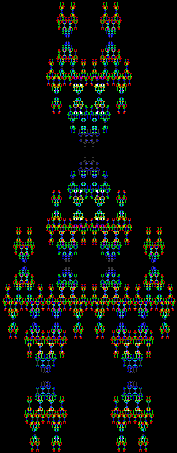
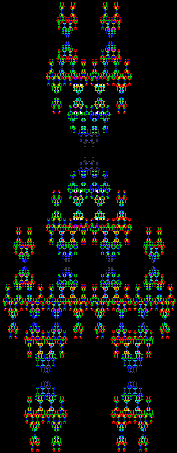
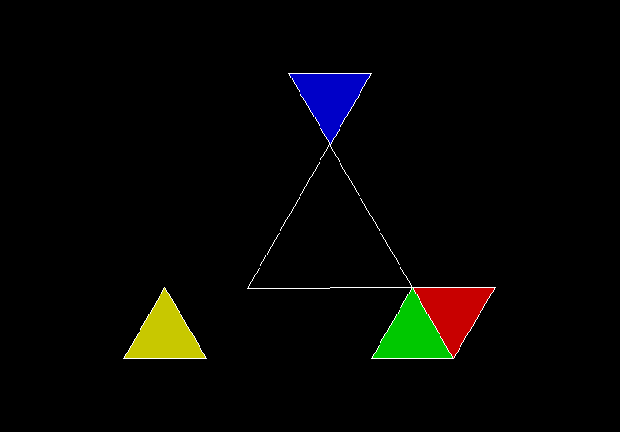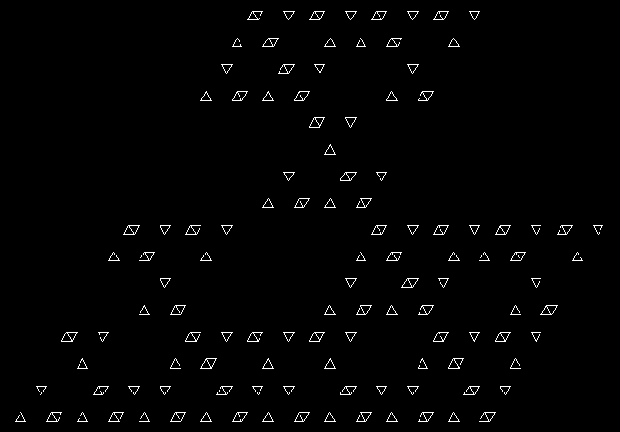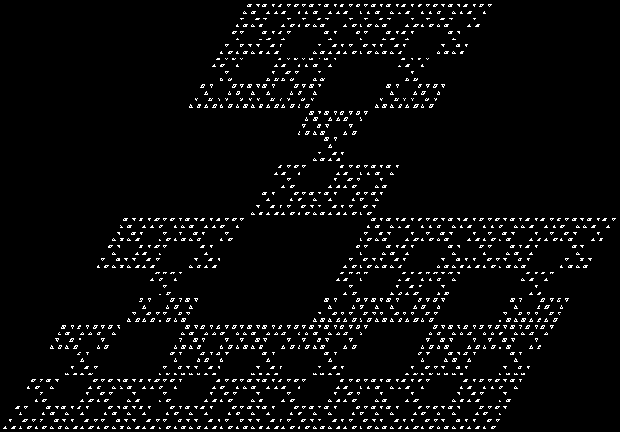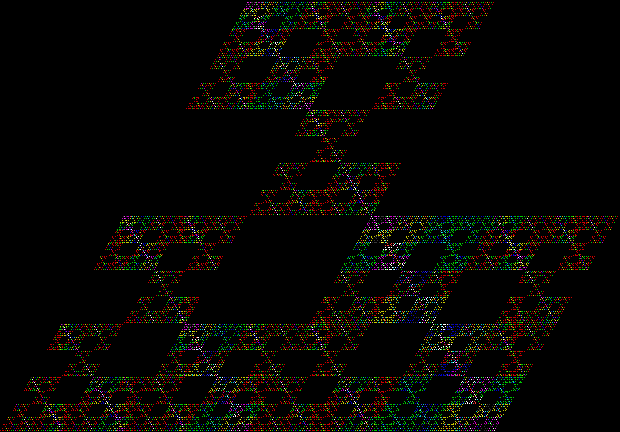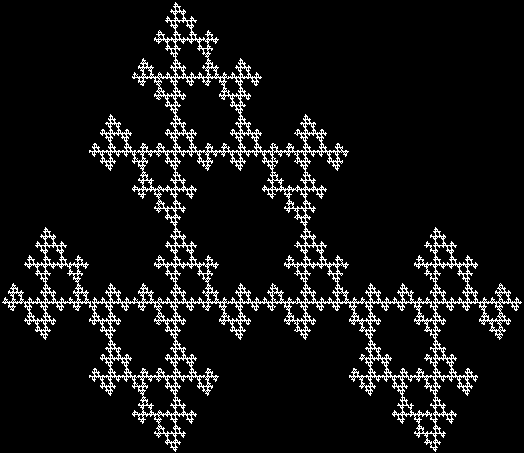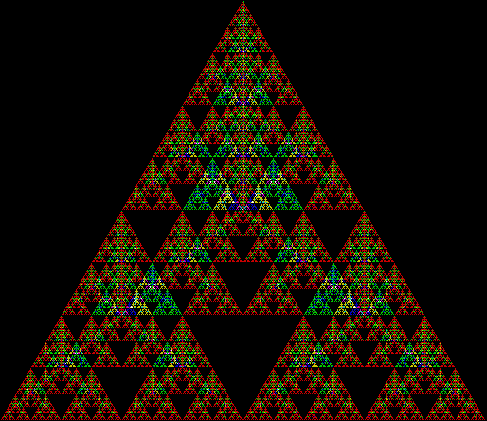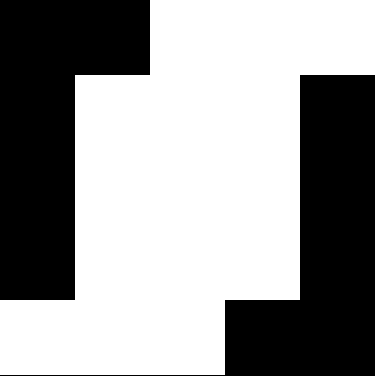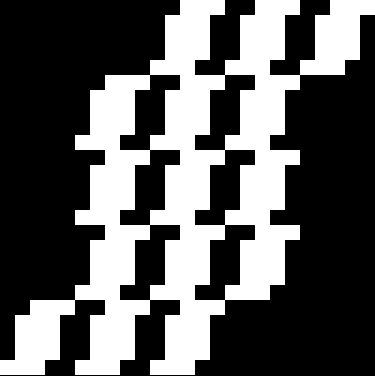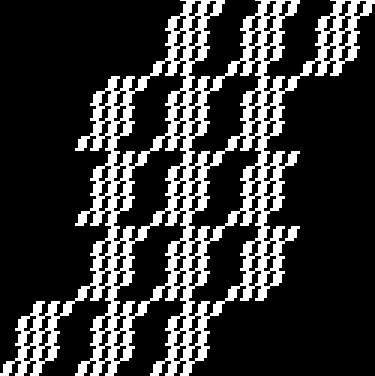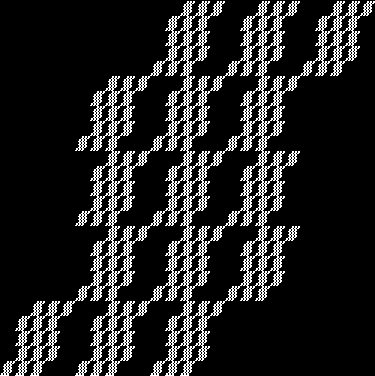In Boldly Breaking the Boundaries, I looked at the use of squares in what I called over-fractals, or fractals whose sub-divisions reproduce the original shape but appear beyond its boundaries. Now I want to look at over-fractals using triangles. They’re less varied than those involving squares, but still include some interesting shapes. This is the space in which sub-triangles can appear, with the central seeding triangle coloured gray: 
Here are some over-fractals based on the pattern above: 
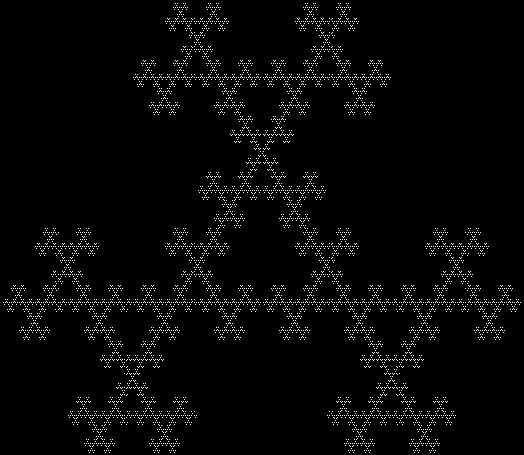
Tag Archives: fractal
Boldly Breaking the Boundaries
In “M.I.P. Trip”, I looked at fractals like this, in which a square is divided repeatedly into a pattern of smaller squares:

As you can see, the sub-squares appear within the bounds of the original square. But what if some of the sub-squares appear beyond the bounds of the original square? Then a new family of fractals is born, the over-fractals:
M.i.P. Trip
The Latin phrase multum in parvo means “much in little”. It’s a good way of describing the construction of fractals, where the application of very simple rules can produce great complexity and beauty. For example, what could be simpler than dividing a square into smaller squares and discarding some of the smaller squares?
Yet repeated applications of divide-and-discard can produce complexity out of even a 2×2 square. Divide a square into four squares, discard one of the squares, then repeat with the smaller squares, like this:
Increase the sides of the square by a little and you increase the number of fractals by a lot. A 3×3 square yields these fractals:
And the 4×4 and 5×5 fractals yield more:

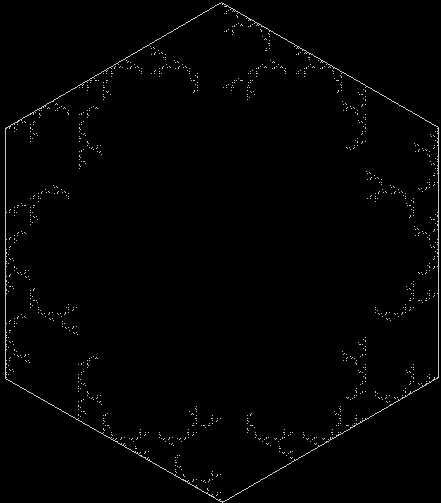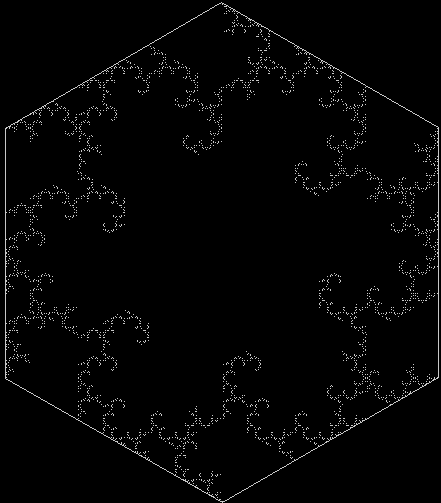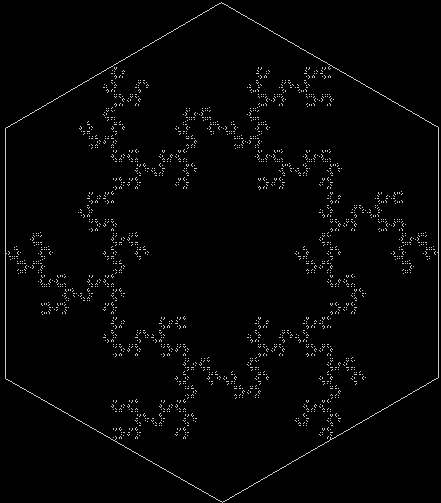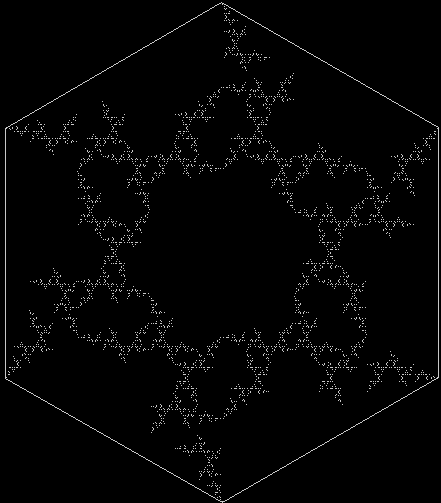
The Hex Fractor
A regular hexagon can be divided into six equilateral triangles. An equilateral triangle can be divided into three more equilateral triangles and a regular hexagon. If you discard the three triangles and repeat, you create a fractal, like this:

Adjusting the sides of the internal hexagon creates new fractals:


Discarding a hexagon after each subdivision creates new shapes:



And you can start with another regular polygon, divide it into triangles, then proceed with the hexagons:

Hextra Texture
A hexagon can be divided into six equilateral triangles. An equilateral triangle can be divided into a hexagon and three more equilateral triangles. These simple rules, applied again and again, can be used to create fractals, or shapes that echo themselves on smaller and smaller scales.
Previously pre-posted (please peruse):
Fractal Fourmulas
Go with the Floe
Fractals are shapes that contain copies of themselves on smaller and smaller scales. There are many of them in nature: ferns, trees, frost-flowers, ice-floes, clouds and lungs, for example. Fractals are also easy to create on a computer, because you all need do is take a single rule and repeat it at smaller and smaller scales. One of the simplest fractals follows this rule:
1. Take a line of length l and find the midpoint.
2. Erect a new line of length l x lm on the midpoint at right angles.
3. Repeat with each of the four new lines (i.e., the two halves of the original line and the two sides of the line erected at right angles).
When lm = 1/3, the fractal looks like this:
(Please open image in a new window if it fails to animate)
When lm = 1/2, the fractal is less interesting:
But you can adjust rule 2 like this:
2. Erect a new line of length l x lm x lm1 on the midpoint at right angles.
When lm1 = 1, 0.99, 0.98, 0.97…, this is what happens:
The fractals resemble frost-flowers on a windowpane or ice-floes on a bay or lake. You can randomize the adjustments and angles to make the resemblance even stronger:

Ice floes (see Owen Kanzler)

Frost on window (see Kenneth G. Libbrecht)
Know Your Limaçons
 The Penguin Dictionary of Curious and Interesting Geometry, David Wells (1991)
The Penguin Dictionary of Curious and Interesting Geometry, David Wells (1991)
Mathematics is an ocean in which a child can paddle and an elephant can swim. Or a whale, indeed. This book, a sequel to Wells’ excellent Penguin Dictionary of Curious and Interesting Mathematics, is suitable for both paddlers and plungers. Plumbers, even, because you can dive into some very deep mathematics here.
Far too deep for me, I have to admit, but I can wade a little way into the shallows and enjoy looking further out at what I don’t understand, because the advantage of geometry over number theory is that it can appeal to the eye even when it baffles the brain. If this book is more expensive than its prequel, that’s because it needs to be. It’s a paperback, but a large one, to accommodate the illustrations.
Fortunately, plenty of them appeal to the eye without baffling the brain, like the absurdly simple yet mindstretching Koch snowflake. Take a triangle and divide each side into thirds. Erect another triangle on each middle third. Take each new line of the shape and do the same: divide into thirds, erect another triangle on the middle third. Then repeat. And repeat. For ever.
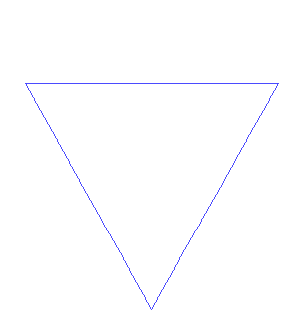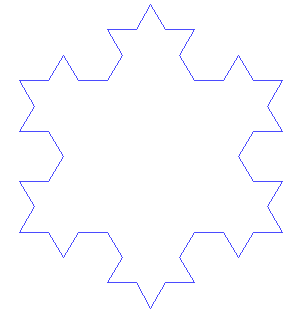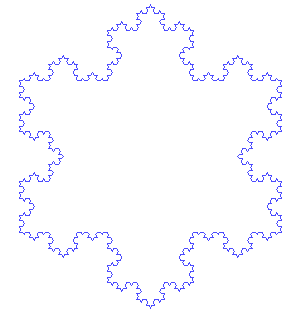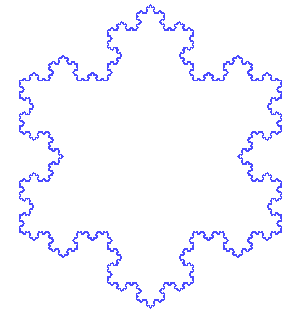
A Koch snowflake (from Wikipedia)
The result is a shape with a finite area enclosed by an infinite perimeter, and it is in fact a very early example of a fractal. Early in this case means it was invented in 1907, but many of the other beautiful shapes and theorems in this book stretch back much further: through Étienne Pascal and his oddly organic limaçon (which looks like a kidney) to the ancient Greeks and beyond. Some, on the other hand, are very modern, and this book was out-of-date on the day it was printed. Despite the thousands of years devoted by mathematicians to shapes and the relationship between them, new discoveries are being made all the time. Knots have probably been tied by human beings for as long as human beings have existed, but we’ve only now started to classify them properly and even find new uses for them in biology and physics.
Which is not to say knots are not included here, because they are. But even the older geometry Wells looks at would be enough to keep amateur and recreational mathematicians happy for years, proving, re-creating, and generalizing as they work their way through variations on all manner of trigonomic, topological, and tessellatory themes.
Previously pre-posted (please peruse):
• Poulet’s Propeller — discussion of Wells’ Penguin Dictionary of Curious and Interesting Numbers (1986)
O Apollo
One of Swinburne’s most powerful, but least-known, poems is “The Last Oracle”, from Poems and Ballads, Second Series (1878). A song in honour of the god Apollo, it begins in lamentation:
Years have risen and fallen in darkness or in twilight,
Ages waxed and waned that knew not thee nor thine,
While the world sought light by night and sought not thy light,
Since the sad last pilgrim left thy dark mid shrine.
Dark the shrine and dumb the fount of song thence welling,
Save for words more sad than tears of blood, that said:
Tell the king, on earth has fallen the glorious dwelling,
And the watersprings that spake are quenched and dead.
Not a cell is left the God, no roof, no cover
In his hand the prophet laurel flowers no more.
And ends in exultation:
For thy kingdom is past not away,
Nor thy power from the place thereof hurled;
Out of heaven they shall cast not the day,
They shall cast not out song from the world.
By the song and the light they give
We know thy works that they live;
With the gift thou hast given us of speech
We praise, we adore, we beseech,
We arise at thy bidding and follow,
We cry to thee, answer, appear,
O father of all of us, Paian, Apollo,
Destroyer and healer, hear! (“The Last Oracle”)
The power, grandeur and beauty of this poem remind me of the music of Beethoven. Swinburne is also, on a smaller scale and in a different medium, one of the geniuses of European art. He and Beethoven were both touched by Apollo, but Apollo was more than the god of music and poetry: he also presided mathematics. But then mathematics is much more visible, or audible, in music and poetry than it is in other arts. Rhythm, harmony, scansion, melody and rhyme are mathematical concepts. Music is built of notes, poetry of stresses and rhymes, and the rules governing them are easier to formalize than those governing, say, sculpture or prose. Nor do poetry and music have to make sense or convey explicit meaning like other arts. That’s why I think a shape like this is closer to poetry or music than it is to painting:
(Image from Wikipedia.)
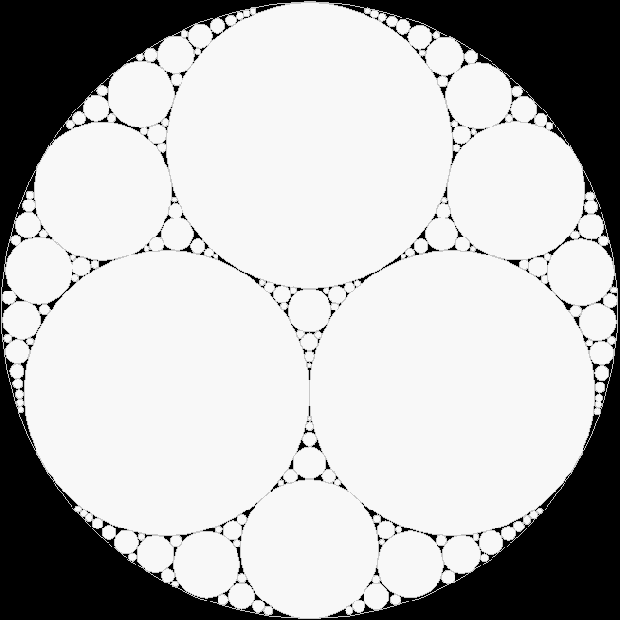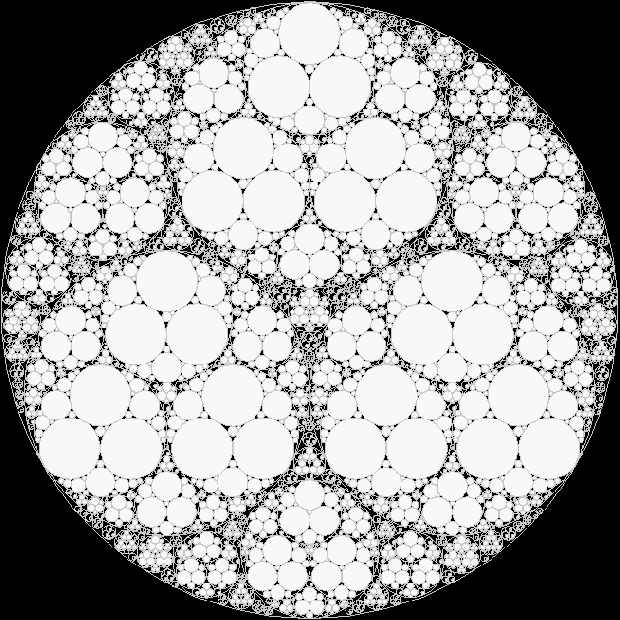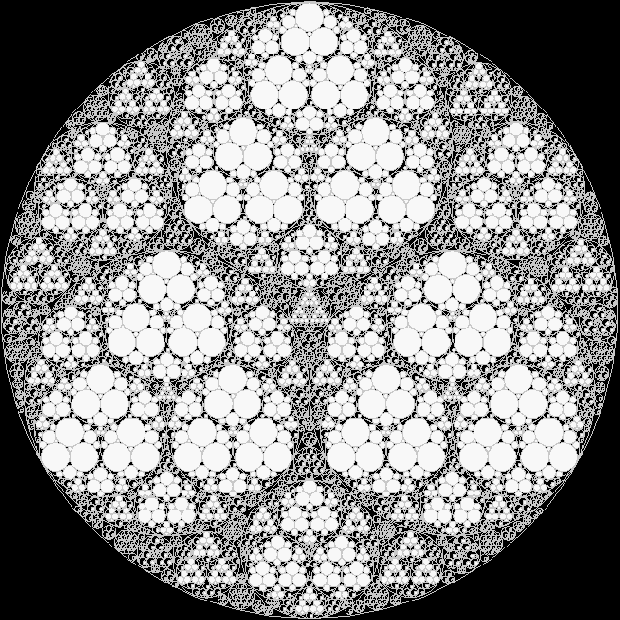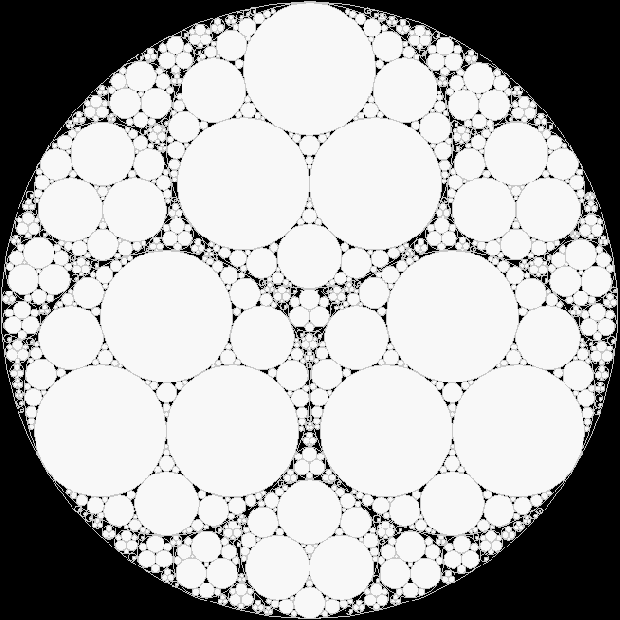
This shape has formal structure and beauty, but it has no explicit meaning. Its name has a divine echo: the Apollonian gasket or net, named after the Greek mathematician Apollonius of Perga (c.262 BC–c.190 BC), who was named after Apollo, god of music, poetry and mathematics. The Apollonian gasket is a fractal, but the version above is not as fractal as it could be. I wondered what it would look like if, like fleas preying on fleas, circles appeared inside circles, gaskets within gaskets. I haven’t managed to program the shape properly yet, but here is my first effort at an Intra-Apollonian gasket:
(If the image does not animate or looks distorted, please try opening it in a new window)
When the circles are solid, they remind me of ice-floes inside ice-floes:
Simpler gaskets can be interesting too:
Tri Again
All roads lead to Rome, so the old saying goes. But you may get your feet wet, so try the Sierpiński triangle instead. This fractal is named after the Polish mathematician Wacław Sierpiński (1882-1969) and quite a few roads lead there too. You can create it by deleting, jumping or bending, inter alia. Here is method #1:
Divide an equilateral triangle into four, remove the central triangle, do the same to the new triangles.
Here is method #2:
Pick a corner at random, jump half-way towards it, mark the spot, repeat.
And here is method #3:
Bend a straight line into a hump consisting of three straight lines, then repeat with each new line.
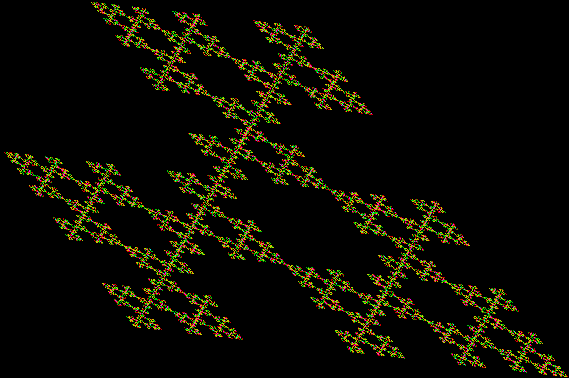
Each method can be varied to create new fractals. Method #3, which is also known as the arrowhead fractal, depends on the orientation of the additional humps, as you can see from the animated gif above. There are eight, or 2 x 2 x 2, ways of varying these three orientations, so eight fractals can be produced if the same combination of orientations is kept at each stage, like this (some are mirror images — if an animated gif doesn’t work, please open it in a new window):
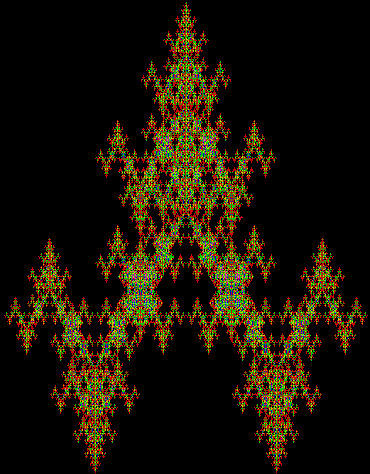
If different combinations are allowed at different stages, the number of different fractals gets much bigger:
• Continuing viewing Tri Again.