Radical Sheet

Thursday, 26th May, 2016 by Krilling for Company in √2, Fractals, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, √2, cross, dividing and discarding, fractal, fractal cross, fractal geometry, fractals, geometry, math, mathematics, maths, paper, paper sizes, radical, radical sheet, recreational math, recreational mathematics, recreational maths, rectangle, rectangles, sheet of paper, square root of two, tessellation, tessellations | Leave a comment

If you take a sheet of standard-sized paper and fold it in half from top to bottom, the folded sheet has the same proportions as the original, namely √2 : 1. In other words, if x = √2 / 2, then 1 / x = √2:

√2 = 1.414213562373…, √2 / 2 = 0.707106781186…, 1 / 0.707106781186… = 1.414213562373…

So you could say that paper has radical sheet (the square or other root of a number is also called its radix and √ is known as the radical sign). When a rectangle has the proportions √2 : 1, it can be tiled with an infinite number of copies of itself, the first copy having ½ the area of the original, the second ¼, the third ⅛, and so on. The radical sheet below is tiled with ten diminishing copies of itself, the final two having the same area:

You can also tile a radical sheet with six copies of itself, two copies having ¼ the area of the original and four having ⅛:

This tiling is when you might say the radical turns crucial, because you can create a fractal cross from it by repeatedly dividing and discarding. Suppose you divide a radical sheet into six copies as above, then discard two of the ⅛-sized rectangles, like this:

Stage 1

Then repeat with the smaller rectangles:

Stage 2

Stage 3

Stage 4

Stage 5

Animated version

Fractile cross

The cross is slanted, but it’s easy to rotate the original rectangle and produce an upright cross:

Performativizing the Polygonic

Tuesday, 17th May, 2016 by Krilling for Company in Fractals, Geometry, Mathematics and tagged animated gif, animated gifs, digits, fractal, fractal geometry, fractals, geometry, heptagons, hexagaon, Hexagons, math, mathematics, maths, Pentagons, performativizing the polygonic, Polygons, recreational math, recreational mathematics, recreational maths, Squares, triangle, Triangles | 4 Comments

Maths is a mountain: you can start climbing in different places and reach the same destination. There are many ways of proving the irrationality of √2 or the infinitude of the primes, for example. But you can also arrive at the same destination by accident. I’ve found that when I use different methods of creating fractals. The same fractals appear, because apparently different algorithms are actually the same underneath.

But different methods can create unique fractals too. I’ve found some new ones by using what might be called point-to-point recursion. For example, there are ten ways to select three vertices from the five vertices of a pentagon: (1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5), (1, 4, 5), (2, 3, 4), (2, 3, 5), (2, 4, 5), (3, 4, 5). Find the midpoint of the first three-point set, (1, 2, 3). Then select two vertices to go with this midpoint, creating a new three-point set, and find the midpoint again. And so on. The process looks like this, with the midpoints shown for all the three-point sets found at each stage:

vertices = 5, choose sets of 3 points, find mid-point of each

At stage 5, the fractal looks like this:

v = 5, p = 3

Note that when pixels are used again, the colour changes. That’s another interesting thing about maths: limits can sometimes produce deeper results. If these fractals were drawn at very high resolution, pixels would only be used once and the colour would never change. As it is, low resolution means that pixels are used again and again. But some are used more than others, which is why interesting colour effects appear.

If the formation of the fractal is animated, it looks like this (with close-ups of even deeper stages):

Here are some more examples:

v = 4 + central point, p = 2 (cf. Fingering the Frigit)

v = 4c, p = 2 (animated)

v = 4, p = 3

v = 5, p = 4

v = 5 + central point, p = 3

v = 5c, p = 4

v = 5c, p = 5

v = 6 + 1 point between each pair of vertices, p = 6

v = 6, p = 2

v = 6, p = 3

v = 6, p = 4

v = 6c, p = 2 (cf. Fingering the Frigit)

v = 6c, p = 3

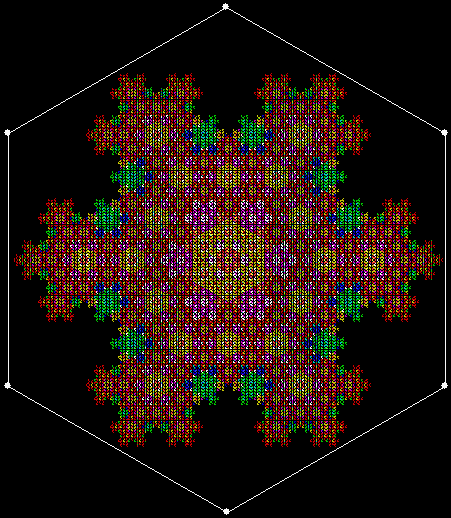
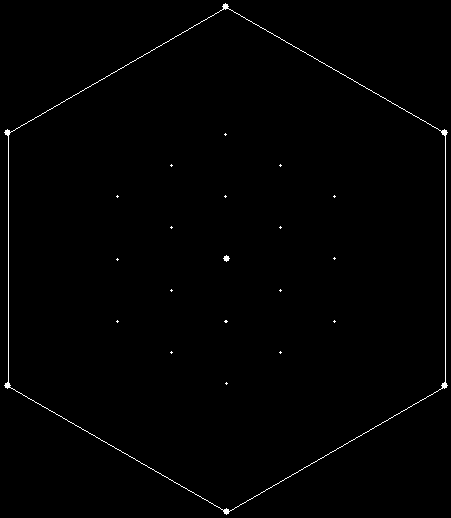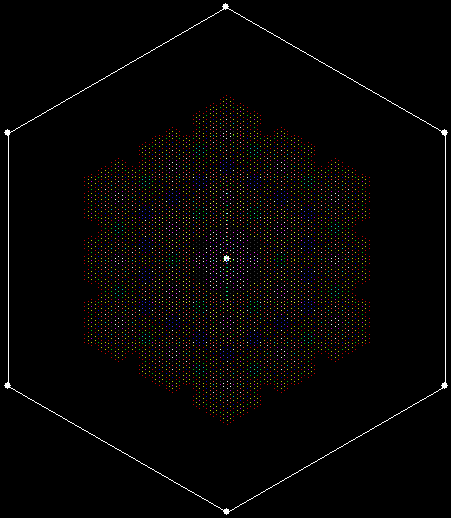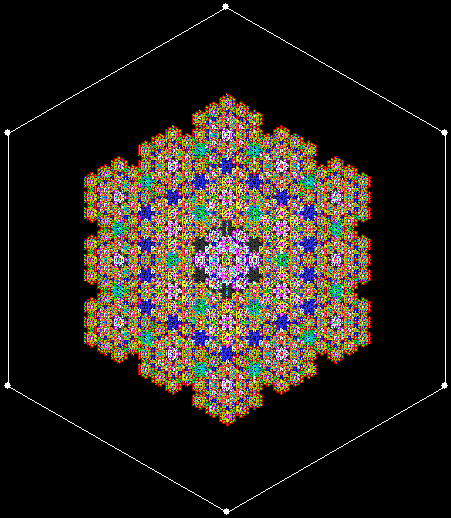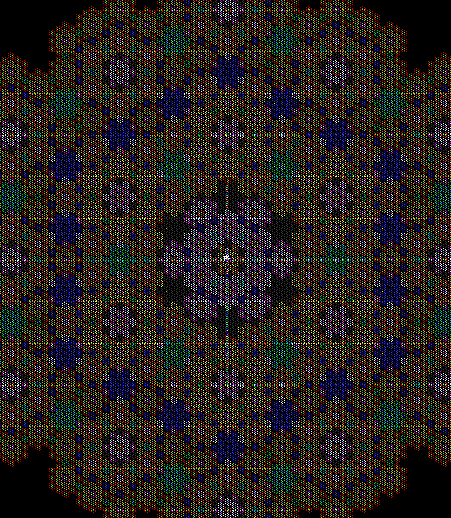
v = 6c, p = 4

v = 7, p = 3

v = 7, p = 4

v = ,7 p = 5

v = 7c, p = 4

v = 3+1, p = 2

v = 3+1, p = 3

v = 3+1, p = 4

v = 3+2, p = 5

v = 3c+1, p = 2

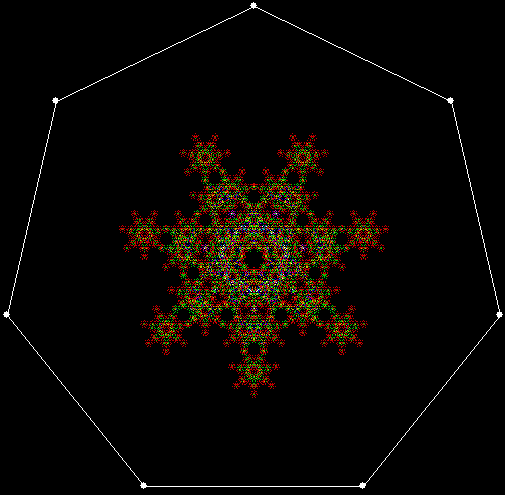
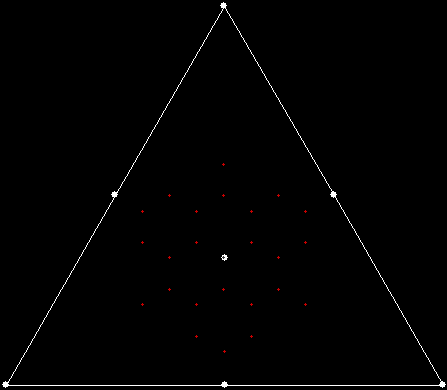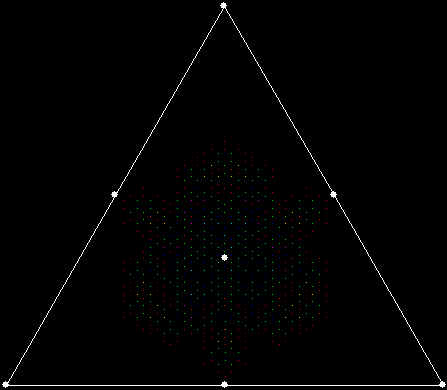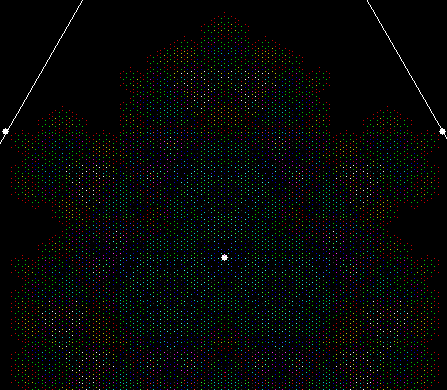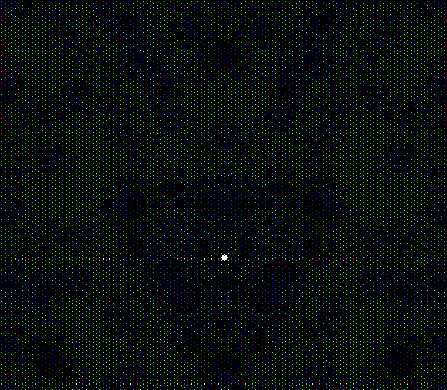
v = 3c+1, p = 4

v = 3c, p = 2

v = 3c, p = 3

v = 4+1, p = 3

v = 4+1, p = 4

v = 4+1, p = 6

v = 4+1, p = 2

v = 4c+1, p = 4

v = 4c, p = 3

v = 5+1, p = 4 (and more)

v = 5, p = 2

Digital Rodeo

Saturday, 7th May, 2016 by Krilling for Company in Base Behavior, Binary numbers, Integer Sequences, Mathematics and tagged Arithmetic, base 10, base 16, base 2, base 3, base 4, base 5, base arithmetic, Base Behavior, base behaviour, base two, binary, counting digits, digit count, digit-counting, digits, hexadecimal, Integer Sequences, math, mathematics, maths, one, ones, recreational math, recreational mathematics, recreational maths, zero, zeros | Leave a comment

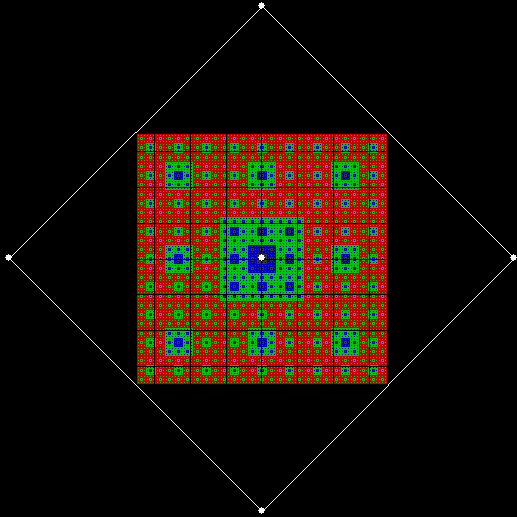
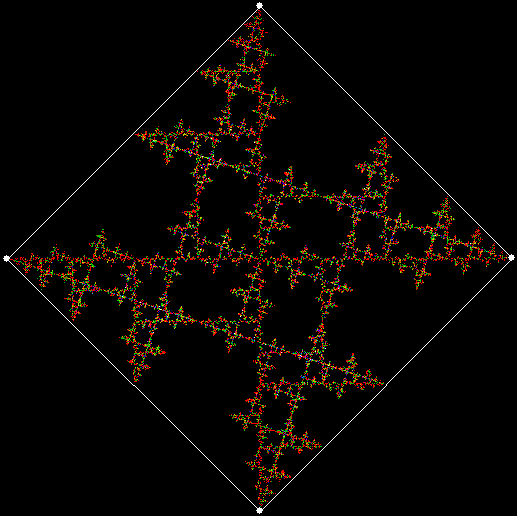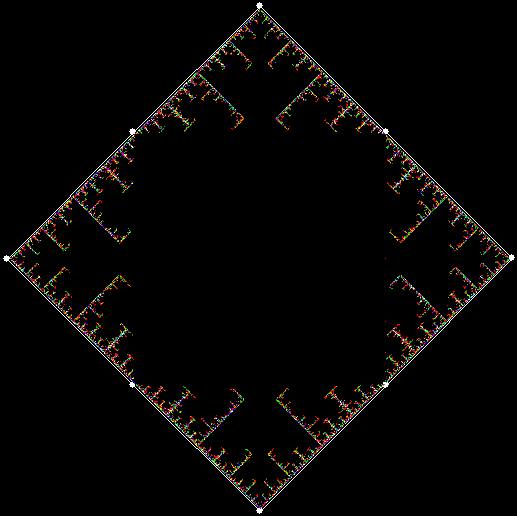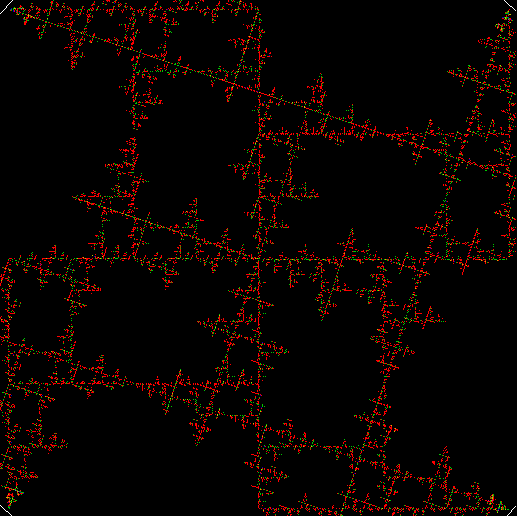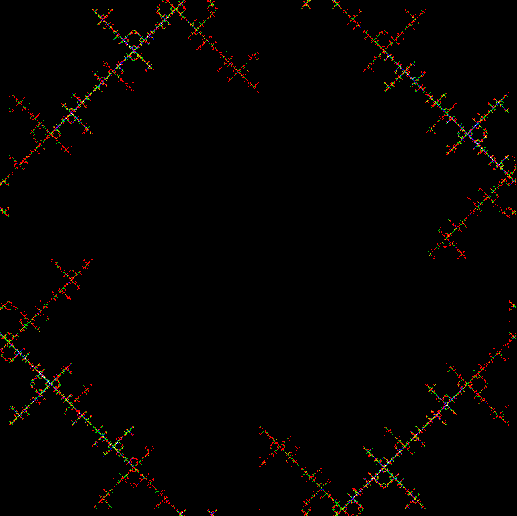
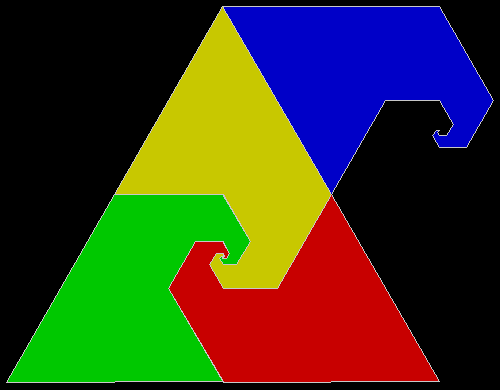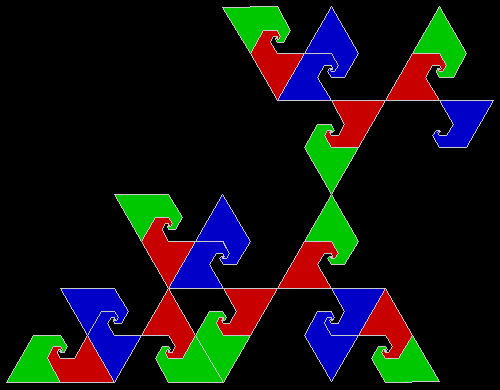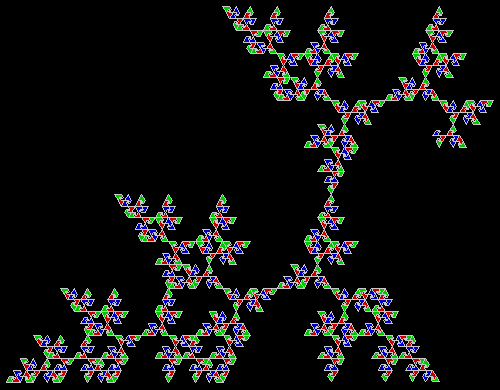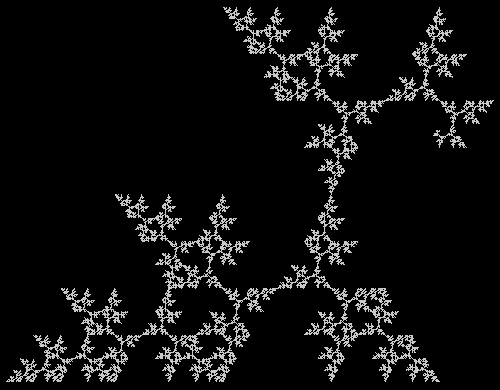
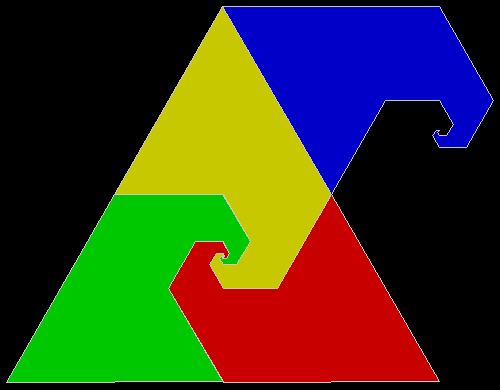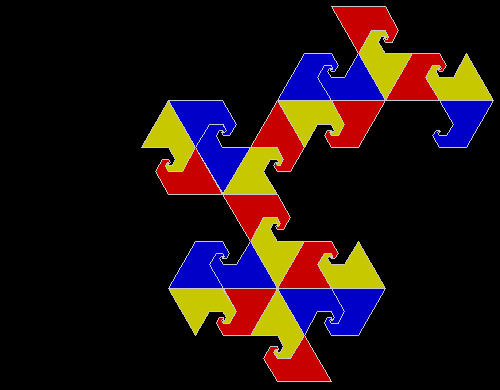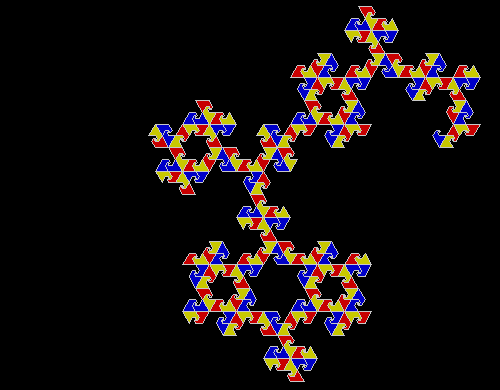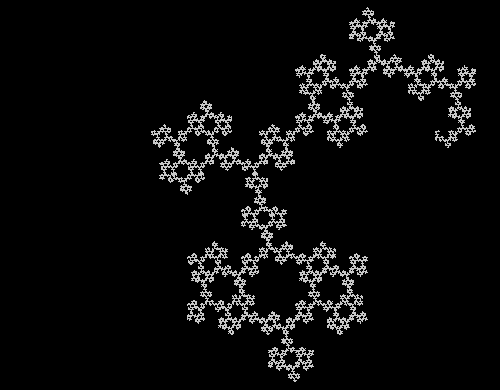
What a difference a digit makes. Suppose you take all representations of n in bases b <= n. When n = 3, the bases are 2 and 3, so 3 = 11 and 10, respectively. Next, count the occurrences of the digit 1:

digitcount(3, digit=1, n=11, 10) = 3

Add this digit-count to 3:

3 + digitcount(3, digit=1, n=11, 10) = 3 + 3 = 6.

Now apply the same procedure to 6. The bases will be 2 to 6:

6 + digitcount(6, digit=1, n=110, 20, 12, 11, 10) = 6 + 6 = 12

The procedure, n = n + digitcount(n,digit=1,base=2..n), continues like this:

12 + digcount(12,dig=1,n=1100, 110, 30, 22, 20, 15, 14, 13, 12, 11, 10) = 12 + 11 = 23
23 + digcount(23,dig=1,n=10111, 212, 113, 43, 35, 32, 27, 25, 23, 21, 1B, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 23 + 21 = 44
44 + digcount(44,dig=1,n=101100, 1122, 230, 134, 112, 62, 54, 48, 44, 40, 38, 35, 32, 2E, 2C, 2A, 28, 26, 24, 22, 20, 1L, 1K, 1J, 1I, 1H, 1G, 1F, 1E, 1D, 1C, 1B, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 44 + 31 = 75

And the sequence develops like this:

3, 6, 12, 23, 44, 75, 124, 202, 319, 503, 780, 1196, 1824, 2766, 4191, 6338, 9546, 14383, 21656, 32562, 48930, 73494, 110361, 165714, 248733, 373303, 560214, 840602, 1261237, 1892269, 2838926, 4258966, 6389157, 9584585, 14377879…

Now try the same procedure using the digit 0: n = n + digcount(n,dig=0,base=2..n). The first step is this:

3 + digcount(3,digit=0,n=11, 10) = 3 + 1 = 4

Next come these:

4 + digcount(4,dig=0,n=100, 11, 10) = 4 + 3 = 7
7 + digcount(7,dig=0,n=111, 21, 13, 12, 11, 10) = 7 + 1 = 8
8 + digcount(8,dig=0,n=1000, 22, 20, 13, 12, 11, 10) = 8 + 5 = 13
13 + digcount(13,dig=0,n=1101, 111, 31, 23, 21, 16, 15, 14, 13, 12, 11, 10) = 13 + 2 = 15
15 + digcount(15,dig=0,n=1111, 120, 33, 30, 23, 21, 17, 16, 15, 14, 13, 12, 11, 10) = 15 + 3 = 18
18 + digcount(18,dig=0,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 18 + 9 = 27
27 + digcount(27,dig=0,n=11011, 1000, 123, 102, 43, 36, 33, 30, 27, 25, 23, 21, 1D, 1C, 1B, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 27 + 7 = 34
34 + digcount(34,dig=0,n=100010, 1021, 202, 114, 54, 46, 42, 37, 34, 31, 2A, 28, 26, 24, 22, 20, 1G, 1F, 1E, 1D, 1C, 1B, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 34 + 8 = 42
42 + digcount(42,dig=0,n=101010, 1120, 222, 132, 110, 60, 52, 46, 42, 39, 36, 33, 30, 2C, 2A, 28, 26, 24, 22, 20, 1K, 1J, 1I, 1H, 1G, 1F, 1E, 1D, 1C, 1B, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 42 + 9 = 51

The sequence develops like this:

3, 4, 7, 8, 13, 15, 18, 27, 34, 42, 51, 59, 62, 66, 80, 94, 99, 111, 117, 125, 132, 151, 158, 163, 173, 180, 204, 222, 232, 244, 258, 279, 292, 307, 317, 324, 351, 364, 382, 389, 400, 425, 437, 447, 454, 466, 475, 483, 494, 509, 517, 536, 553, 566, 576, 612, 637, 649, 669, 679, 693, 712, 728, 753, 768, 801, 822, 835, 849, 862, 869, 883, 895, 906, 923, 932, 943, 949, 957, 967, 975, 999, 1011…

If you compare it with the sequence for digit=1, it appears that digcount(n,dig=1,b=2..n) is always larger than digcount(n,dig=0,b=2..n). That is in fact the case, with one exception, when n = 2:

digcount(2,dig=1,n=10) = 1
digcount(2,dig=0,n=10) = 1

When n = 10 (in base ten), there are twice as many ones as zeros:

digcount(10,dig=1,n=1010, 101, 22, 20, 14, 13, 12, 11, 10) = 10
digcount(10,dig=0,n=1010, 101, 22, 20, 14, 13, 12, 11, 10) = 5

As n gets larger, the difference grows dramatically:

digcount(100,dig=1,base=2..n) = 64
digcount(100,dig=0,base=2..n) = 16

digcount(1000,dig=1,base=2..n) = 533
digcount(1000,dig=0,base=2..n) = 25

digcount(10000,dig=1,base=2..n) = 5067
digcount(10000,dig=0,base=2..n) = 49

digcount(100000,dig=1,base=2..n) = 50140
digcount(100000,dig=0,base=2..n) = 73

digcount(1000000,dig=1,base=2..n) = 500408
digcount(1000000,dig=0,base=2..n) = 102

digcount(10000000,dig=1,base=2..n) = 5001032
digcount(10000000,dig=0,base=2..n) = 134

digcount(100000000,dig=1,base=2..n) = 50003137
digcount(100000000,dig=0,base=2..n) = 160

In fact, digcount(n,dig=1,b=2..n) is greater than the digit-count for any other digit: 0, 2, 3, 4, 5… (with the exception n = 2, as shown above). But digit=0 sometimes beats digits >= 2. For example, when n = 18:

digcount(18,dig=0,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 9
digcount(18,dig=2,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 7
digcount(18,dig=3,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 4
digcount(18,dig=4,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 2
digcount(18,dig=5,n=10010, 200, 102, 33, 30, 24, 22, 20, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 1

But as n gets larger, digcount(0) will fall permanently behind all these digits. However, digcount(0) will always be greater than some digit d, for the obvious reason that some digits only appear when the base is high enough. For example, the hexadecimal digit A (with the decimal value 10) first appears when n = 21:

digcount(21,dig=A,n=10101, 210, 111, 41, 33, 30, 25, 23, 21, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 1 digcount(21,dig=0,n=10101, 210, 111, 41, 33, 30, 25, 23, 21, 1A, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10) = 5

There is a general rule for the n at which digit d first appears, n = 2d + 1 (this doesn’t apply when d = 0 or d = 1):

d = 2, n = 5 = 2*2 + 1
digcount(5,dig=2,n=101, 12, 11, 10) = 1

d = 3, n = 7 = 2*3 + 1
digcount(7,dig=3,n=111, 21, 13, 12, 11, 10) = 1

d = 4, n = 9 = 2*4 + 1
digcount(9,dig=4,n=1001, 100, 21, 14, 13, 12, 11, 10) = 1

d = 5, n = 11 = 2*5 + 1
digcount(11,dig=5,n=1011, 102, 23, 21, 15, 14, 13, 12, 11, 10) = 1

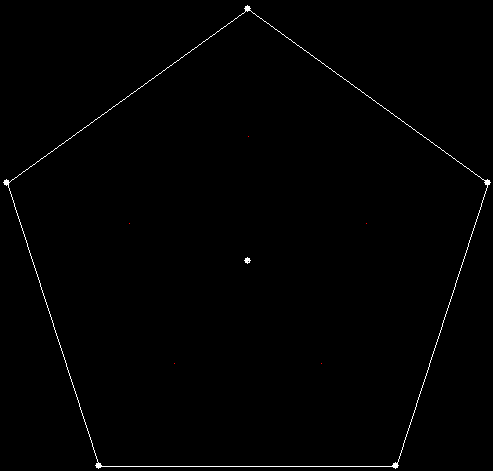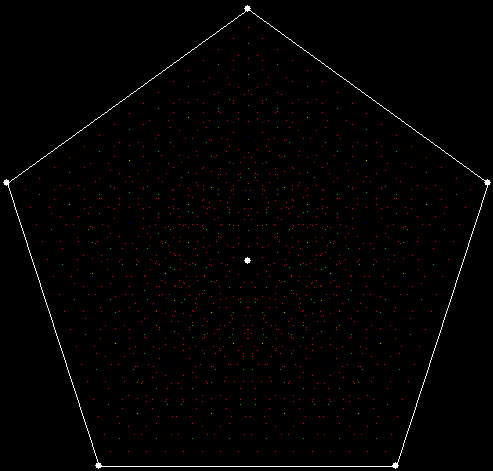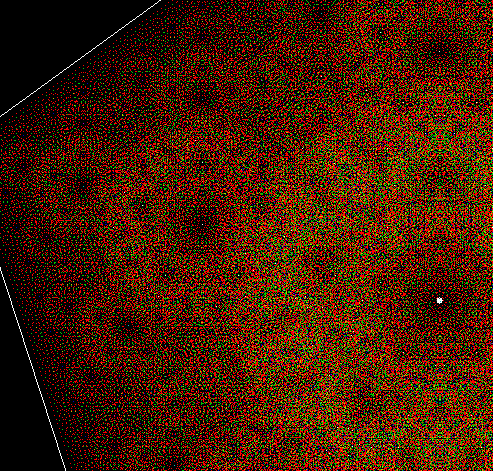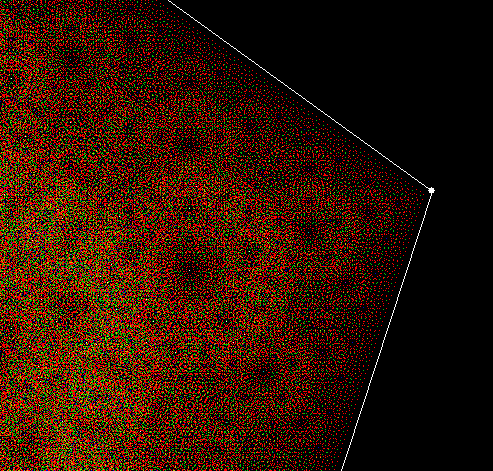
It should be apparent, then, that the digit-count for a particular digit starts at 1 and gets gradually higher. The rate at which the digit-count increases is highest for 1 and lowest for 0, with digits 2, 3, 4, 5… in between:

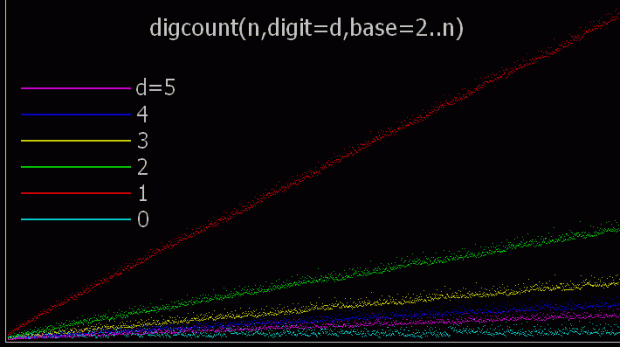
Graph for digcount(n,dig=d,b=2..n)

You could think of the graph as a digital rodeo in which these digits compete with each other. 1 is the clear and permanent winner, 0 the gradual loser. Now recall the procedure introduced at the start: n = n + digcount(n,dig=d,b=2..n). When it’s applied to the digits 0 to 5, these are the sequences that appear:

n = n + digcount(n,dig=0,b=2..n)

2, 3, 4, 7, 8, 13, 15, 18, 27, 34, 42, 51, 59, 62, 66, 80, 94, 99, 111, 117, 125, 132, 151, 158, 163, 173, 180, 204, 222, 232, 244, 258, 279, 292, 307, 317, 324, 351, 364, 382, 389, 400, 425, 437, 447, 454, 466, 475, 483, 494, 509, 517, 536, 553, 566, 576, 612, 637, 649, 669, 679, 693, 712, 728, 753, 768, 801, 822, 835, 849, 862, 869, 883, 895, 906, 923, 932, 943, 949, 957, 967, 975, 999, 1011…

n = n + digcount(n,dig=1,b=2..n)

2, 3, 6, 12, 23, 44, 75, 124, 202, 319, 503, 780, 1196, 1824, 2766, 4191, 6338, 9546, 14383, 21656, 32562, 48930, 73494, 110361, 165714, 248733, 373303, 560214, 840602, 1261237, 1892269, 2838926, 4258966, 6389157, 9584585, 14377879…

n = n + digcount(n,dig=2,b=2..n)

5, 6, 8, 12, 16, 22, 31, 37, 48, 60, 76, 94, 115, 138, 173, 213, 257, 311, 374, 454, 542, 664, 790, 935, 1109, 1310, 1552, 1835, 2167, 2548, 2989, 3509, 4120, 4832, 5690, 6687, 7829, 9166, 10727, 12568, 14697, 17182, 20089, 23470, 27425, 32042, 37477, 43768, 51113, 59687, 69705, 81379, 94998, 110910, 129488, 151153, 176429, 205923, 240331, 280490, 327396, 382067, 445858…

n = n + digcount(n,dig=3,b=2..n)

7, 8, 9, 10, 11, 13, 16, 18, 22, 25, 29, 34, 38, 44, 50, 56, 63, 80, 90, 104, 113, 131, 151, 169, 188, 210, 236, 261, 289, 320, 350, 385, 424, 463, 520, 572, 626, 684, 747, 828, 917, 999, 1101, 1210, 1325, 1446, 1577, 1716, 1871, 2040, 2228, 2429, 2642, 2875, 3133, 3413, 3719, 4044, 4402, 4786, 5196, 5645, 6140, 6673, 7257, 7900, 8582, 9315, 10130, 10998, 11942, 12954, 14058…

n = n + digcount(n,dig=4,b=2..n)

9, 10, 11, 12, 13, 14, 16, 18, 20, 23, 25, 28, 34, 41, 44, 52, 61, 67, 74, 85, 92, 102, 113, 121, 134, 148, 170, 184, 208, 229, 253, 269, 287, 306, 324, 356, 386, 410, 439, 469, 501, 531, 565, 604, 662, 703, 742, 794, 845, 895, 953, 1007, 1062, 1127, 1188, 1262, 1336, 1421, 1503, 1585, 1676, 1777, 1876, 2001, 2104, 2249, 2375, 2502, 2636, 2789, 2938, 3102, 3267, 3444, 3644, 3868, 4099…

n = n + digcount(n,dig=5,b=2..n)

11, 12, 13, 14, 15, 16, 17, 19, 21, 23, 26, 28, 29, 33, 37, 41, 48, 50, 55, 60, 64, 67, 72, 75, 83, 91, 96, 102, 107, 118, 123, 129, 137, 151, 159, 171, 180, 192, 202, 211, 224, 233, 251, 268, 280, 296, 310, 324, 338, 355, 380, 401, 430, 455, 488, 511, 536, 562, 584, 607, 638, 664, 692, 718, 748, 778, 807, 838, 874, 911, 951, 993, 1039, 1081, 1124, 1166, 1216, 1264, 1313, 1370, 1432…

Polymorphous Perverticity

Thursday, 28th Apr, 2016 by Krilling for Company in Fractals, Geometry, Mathematics and tagged animated gif, animated gifs, fractal, fractal geometry, fractals, geometry, Hexagons, math, mathematics, maths, Pentagons, polygon fractals, polygonal fractals, polygonic performativity, Polygons, premier purveyor, recreational math, recreational mathematics, recreational maths, Sierpiński pentagon, Sierpiński triangle, Squares, triangle, Triangles, vertex, vertices | Leave a comment

As I’ve explained before on Overlord of the Über-Feral, the planet’s premier purveyor of polygonic performativity (probably (possibly (perspectivistically))), it works with triangles and pentagons, but not with squares. And what is “it”? A simple procedure in which you create a polygon, choose a point inside it, then repeatedly move half-way towards a vertex chosen at random, marking each new position as you go.

When the polygon has three vertices, you get a Sierpiński triangle. When it has five, you get what might be called a Sierpiński pentagon. When it has four, you get nothing. Or rather: you get everything, because the whole interior of the square gradually fills with points. But, as I’ve also explained before, there’s a simple way to change this. You can adapt the procedure so that a vertex can’t be chosen twice in a row, and so on.

When the rule is “No vertex twice in a row”, you get this fractal (colours change as a pixel is selected again):

But you can also use what might be a vertex increment, or vi, whereby you disallow vertices that are next to the previously chosen vertex, or two positions away, and so on. When the rule is “No vertex twice in a row”, the disallowed vertex is (v + 0), that is, vi = 0. If vi = 2 and the rule is disallow(v + 2), this fractal appears (when vi = 1, there’s no fractal):

v = 4, vi = 2

You can extend these rules to apply not just to the previously chosen vertex, but also to the vertex chosen before that. Here are some fractals produced by the rule disallow(v[1] + vi[1], v[2] + vi[2]), where v[1] is the vertex previously chosen and v[2] is the vertex chosen before that:

v = 4, vi[1] = 1, vi[2] = 2

v = 4, vi[1] = 2, vi[2] = 0

v = 4, vi[1] = 2, vi[2] = 1

v = 4, vi[1] = 2, vi[2] = 2

And here are some fractals produced by the rule disallow(v[1] + vi[1], v[2] + vi[2], v[3] + vi[3]):

v = 4, vi[1] = 1, vi[2] = 1, vi[3] = 0

v = 4, vi[1] = 1, vi[2] = 1, vi[3] = 2

Applying these rules to pentagons rather than squares doesn’t produce such a dramatic difference, because the original procedure – choose any vertex at random, taking no account of previous choices – produces a fractal when v = 5, as noted above, but not when v = 4. Nevertheless, here are some fractals for v > 4:

v = 5, vi = 0

v = 5, vi = 1

v = 5, vi = 2

v = 5, vi[1] = 0, vi[2] = 0

v = 5, vi[1] = 1, vi[2] = 0

v = 5, vi[1] = 2, vi[2] = 0

v = 5, vi[1] = 1, vi[2] = 1

v = 5, vi[1] = 1, vi[2] = 1, vi[3] = 1

v = 5, vi = various

v = 6, vi = 1

Fingering the Frigit

Thursday, 24th Mar, 2016 by Krilling for Company in Biology, Fractals, Geometry, Mathematics and tagged anatomy, animated gif, animated gifs, base 5, base 6, digits, fingers, fractal, fractal anatomy, fractal biology, fractal geometry, fractals, frigit, frigits, geometry, heptagons, Hexagons, human anatomy, integers, math, mathematics, maths, nonagons, numbers as fractals, octagons, Pentagons, Polygons, recreational math, recreational mathematics, recreational maths, Squares, triangle, Triangles | Leave a comment

Fingers are fractal. Where a tree has a trunk, branches and twigs, a human being has a torso, arms and fingers. And human beings move in fractal ways. We use our legs to move large distances, then reach out with our arms over smaller distances, then move our fingers over smaller distances still. We’re fractal beings, inside and out, brains and blood-vessels, fingers and toes.

But fingers are fractal are in another way. A digit – digitus in Latin – is literally a finger, because we once counted on our fingers. And digits behave like fractals. If you look at numbers, you’ll see that they contain patterns that echo each other and, in a sense, recur on smaller and smaller scales. The simplest pattern in base 10 is (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). It occurs again and again at almost very point of a number, like a ten-hour clock that starts at zero-hour:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9…
10, 11, 12, 13, 14, 15, 16, 17, 18, 19…
200… 210… 220… 230… 240… 250… 260… 270… 280… 290…

These fractal patterns become visible if you turn numbers into images. Suppose you set up a square with four fixed points on its corners and a fixed point at its centre. Let the five points correspond to the digits (1, 2, 3, 4, 5) of numbers in base 6 (not using 0, to simplify matters):

1, 2, 3, 4, 5, 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55, 61, 62, 63, 64, 65… 2431, 2432, 2433, 2434, 2435, 2441, 2442, 2443, 2444, 2445, 2451, 2452…

Move between the five points of the square by stepping through the individual digits of the numbers in the sequence. For example, if the number is 2451, the first set of successive digits is (2, 4), so you move to a point half-way between point 2 and point 4. Next come the successive digits (4, 5), so you move to a point half-way between point 4 and point 5. Then come (5, 1), so you move to a point half-way between point 5 and point 1.

When you’ve exhausted the digits (or frigits) of a number, mark the final point you moved to (changing the colour of the pixel if the point has been occupied before). If you follow this procedure using a five-point square, you will create a fractal something like this:
$fractal4_1single$

$fractal4_1$
A pentagon without a central point using numbers in a zero-less base 7 looks like this:
$fractal5_0single$

$fractal5_0$
A pentagon with a central point looks like this:
$fractal5_1single$

$fractal5_1$
Hexagons using a zero-less base 8 look like this:
$fractal6_1single$

$fractal6_1$

$fractal6_0single$

$fractal6_0$
But the images above are just the beginning. If you use a fixed base while varying the polygon and so on, you can create images like these (here is the program I used):
$fractal4$

$fractal5$

$fractal6789$

Amateur ’Grammatics

Monday, 14th Mar, 2016 by Krilling for Company in Base Behavior, Mathematics, Psychology and tagged anagrams, base 10, base 2, base 3, bases, digital anagrams, digits, escape from reality, machine code, math, mathematics, maths, number anagrams, number bases, number of digits, number-length, numbers, psychology of mathematicians, psychology of mathematics, recreational math, recreational mathematics, recreational maths, Stanislaw Ulam | Leave a comment

There is much more to mathematics than mathematics. Like a tree, it has deep roots. Like a tree, it’s affected by its environment. Philosophy of mathematics is concerned with the roots. Psychology of mathematics is concerned with the environment.

On Planet Earth, the environment is human beings. What attracts men and women to the subject? What makes them good or bad at it?And so on. One interesting answer to the first question was supplied by the mathematician Stanislaw Ulam (1909-84), who wrote this in his autobiography:

“In many cases, mathematics is an escape from reality. The mathematician finds his own monastic niche and happiness in pursuits that are disconnected from external affairs. Some practice it as if using a drug.” – Adventures of a Mathematician (1983)

That’s certainly part of maths’ appeal to me: as an escape from reality, or an escape from one reality into another (and deeper). Real life is messy. Maths isn’t, unless you want it to be. But you can find parallels between maths and real life too. In real life, people collect things that they find attractive or interesting: stamps, sea-shells, gems, cigarette-cards, beer-cans and so on. You can collect things in maths too: interesting numbers and number patterns. Recreational maths can feel like looking on a beach for attractive shells and pebbles.

Here’s a good example: digital anagrams, or numbers in different bases whose digits are the same but re-arranged. For example, 13 in base 10 equals 31 in base 4, because 13 = 3 * 4 + 1. To people with the right kind of mind, that’s an interesting and attractive pattern. There are lots more anagrams like that:

1045 = 4501 in base 6
1135 = 5131 in base 6

23 = 32 in base 7
46 = 64 in base 7

1273 = 2371 in base 8
1653 = 3165 in base 8

158 = 185 in base 9
227 = 272 in base 9

196 = 169 in base 11
283 = 238 in base 11

2193 = 1329 in base 12
6053 = 3605 in base 12

43 = 34 in base 13
86 = 68 in base 13

But triple anagrams, involving three bases, seem even more attractive:

913 = 391 in base 16 = 193 in base 26
103462 = 610432 in base 7 = 312046 in base 8
245183 = 413285 in base 9 = 158234 in base 11

And that’s just looking in base 10. If you include all bases, the first double anagram is in fact 21 in base 3 = 12 in base 5 (equals 7 in base 10). The first triple anagram is this:

2C1 in base 13 = 1C2 in base 17 = 12C in base 21 (equals 495 in base 10)

But are there quadruple anagrams, quintuple anagrams and higher? I don’t know. I haven’t found any and it gets harder and harder to search for them, because the bigger n gets, the more bases there are to check. However, I can say one thing for certain: in any given base, anagrams eventually disappear.

To understand why, consider the obvious fact that anagrams have to have the same number of digits in different bases. But the number of digits is a function of the powers of the base. That is, the triple anagram 103462 (see above) has six digits in bases 7, 8 and 10 because 7^5 < 103462 < 7^6, 8^5 < 103462 < 8^6 and 10^5 < 103462 < 10^6. Similarly, the triple anagram 245183 (ditto) has six digits in bases 9, 10 and 11 because 9^5 < 245183 < 9^6, 10^5 < 245183 < 10^6 and 11^5 < 245183 < 11^6:

7^5 < 103462 < 7^6
16807 < 103462 < 117649
8^5 < 103462 < 8^6
32768 < 103462 < 262144
10^5 < 103462 < 10^6
100000 < 103462 < 1000000
9^5 < 245183 < 9^6
59049 < 245183 < 531441
10^5 < 245183 < 10^6
100000 < 245183 < 1000000
11^5 < 245183 < 11^6
161051 < 245183 < 1771561

In other words, for some n the number-lengths of bases 7 and 8 overlap the number-lengths of base 10, which overlap the number-lengths of bases 9 and 11. But eventually, as n gets larger, the number-lengths of base 10 will fall permanently below the number-lengths of bases 7, 8 and 9, just as the number-lengths of base 11 will fall permanently below the number-lengths of base 10.

To see this in action, consider the simplest example: number-lengths in bases 2 and 3. There is no anagram involving these two bases, because only two numbers have the same number of digits in both: 1 and 3 = 11 in base 2 = 10 in base 3. After that, n in base 2 always has more digits than n in base 3:

2^0 = 1 in base 2 (number-length=1) = 1 in base 3 (l=1)
2^1 = 2 = 10 in base 2 (number-length=2) = 2 in base 3 (l=1)
2^2 = 4 = 100 in base 2 (l=3) = 11 in base 3 (l=2)
2^3 = 8 = 1000 in base 2 = 22 in base 3 (l=2)
2^4 = 16 = 10000 in base 2 = 121 in base 3 (l=3)
2^5 = 32 = 1012 in base 3 (l=4)
2^6 = 64 = 2101 in base 3 (l=4)
2^7 = 128 = 11202 in base 3 (l=5)
2^8 = 256 = 100111 in base 3 (l=6)
2^9 = 512 = 200222 in base 3 (l=6)
2^10 = 1024 = 1101221 in base 3 (l=7)

Now consider bases 3 and 4. Here is an anagram using these bases: 211 in base 3 = 112 in base 4 = 22. There are no more anagrams and eventually there’s no more chance for them to occur, because this happens as n gets larger:

3^0 = 1 in base 3 (number-length=1) = 1 in base 4 (l=1)
3^1 = 3 = 10 in base 3 (number-length=2) = 3 in base 4 (l=1)
3^2 = 9 = 100 in base 3 (l=3) = 21 in base 4 (l=2)
3^3 = 27 = 1000 in base 3 (l=4) = 123 in base 4 (l=3)
3^4 = 81 = 10000 in base 3 (l=5) = 1101 in base 4 (l=4)
3^5 = 243 = 100000 in base 3 (l=6) = 3303 in base 4 (l=4)
3^6 = 729 = 23121 in base 4 (l=5)
3^7 = 2187 = 202023 in base 4 (l=6)
3^8 = 6561 = 1212201 in base 4 (l=7)
3^9 = 19683 = 10303203 in base 4 (l=8)
3^10 = 59049 = 32122221 in base 4 (l=8)
3^11 = 177147 = 223033323 in base 4 (l=9)
3^12 = 531441 = 2001233301 in base 4 (l=10)
3^13 = 1594323 = 12011033103 in base 4 (l=11)
3^14 = 4782969 = 102033231321 in base 4 (l=12)
3^15 = 14348907 = 312233021223 in base 4 (l=12)
3^16 = 43046721 = 2210031131001 in base 4 (l=13)
3^17 = 129140163 = 13230220113003 in base 4 (l=14)
3^18 = 387420489 = 113011321011021 in base 4 (l=15)
3^19 = 1162261467 = 1011101223033123 in base 4 (l=16)
3^20 = 3486784401 = 3033311001232101 in base 4 (l=16)

When n is sufficiently large, it always has fewer digits in base 4 than in base 3. And the gap gets steadily bigger. When n doesn’t have the same number of digits in two bases, it can’t be an anagram. A similar number-length gap eventually appears in bases 4 and 5, but the anagrams don’t run out as quickly there:

103 in base 5 = 130 in base 4 = 28
1022 in base 5 = 2021 in base 4 = 137
1320 in base 5 = 3102 in base 4 = 210
10232 in base 5 = 22310 in base 4 = 692
10332 in base 5 = 23031 in base 4 = 717
12213 in base 5 = 32211 in base 4 = 933
100023 in base 5 = 301002 in base 4 = 3138
100323 in base 5 = 302031 in base 4 = 3213
102131 in base 5 = 311120 in base 4 = 3416
102332 in base 5 = 312023 in base 4 = 3467
103123 in base 5 = 313102 in base 4 = 3538
1003233 in base 5 = 3323010 in base 4 = 16068

Base 10 isn’t exempt. Eventually it must outshrink base 9 and be outshrunk by base 11, so what is the highest 9:10 anagram and highest 10:11 anagram? I don’t know: my maths isn’t good enough for me to find out quickly. But using machine code, I’ve found these large anagrams:

205888888872731 = 888883178875022 in base 9
1853020028888858 = 8888888525001032 in base 9
16677181388880888 = 88888888170173166 in base 9

999962734025 = 356099992472 in base 11
9999820360965 = 3205999998606 in base 11
99999993520348 = 29954839390999 in base 11

Note how the digits of n in the lower base are increasing as the digits of n in the higher base are decreasing. Eventually, n in the lower base will always have more digits than n in the higher base. When that happens, there will be no more anagrams.

Some triple anagrams

2C1 in base 13 = 1C2 in base 17 = 12C in base 21 (n=495 = 3^2*5*11)
912 in base 10 = 219 in base 21 = 192 in base 26 (2^4*3*19)
913 in base 10 = 391 in base 16 = 193 in base 26 (11*83)
4B2 in base 15 = 42B in base 16 = 24B in base 22 (n=1067 = 11*97)
5C1 in base 17 = 51C in base 18 = 1C5 in base 35 (n=1650 = 2*3*5^2*11)
3L2 in base 26 = 2L3 in base 31 = 23L in base 35 (n=2576 = 2^4*7*23)
3E1 in base 31 = 1E3 in base 51 = 13E in base 56 (n=3318 = 2*3*7*79)
531 in base 29 = 351 in base 37 = 135 in base 64 (n=4293 = 3^4*53)
D53 in base 18 = 53D in base 29 = 35D in base 37 (n=4305 = 3*5*7*41)
53I in base 29 = 3I5 in base 35 = 35I in base 37 (n=4310 = 2*5*431)
825 in base 25 = 582 in base 31 = 258 in base 49 (n=5055 = 3*5*337)
6S2 in base 31 = 2S6 in base 51 = 26S in base 56 (n=6636 = 2^2*3*7*79)
D35 in base 23 = 5D3 in base 36 = 3D5 in base 46 (n=6951 = 3*7*331)
3K1 in base 49 = 31K in base 52 = 1K3 in base 81 (n=8184 = 2^3*3*11*31)
A62 in base 29 = 6A2 in base 37 = 26A in base 64 (n=8586 = 2*3^4*53)
9L2 in base 30 = 92L in base 31 = 2L9 in base 61 (n=8732 = 2^2*37*59)
3W1 in base 49 = 1W3 in base 79 = 13W in base 92 (n=8772 = 2^2*3*17*43)
G4A in base 25 = AG4 in base 31 = 4AG in base 49 (n=10110 = 2*3*5*337)
J10 in base 25 = 1J0 in base 100 = 10J in base 109 (n=11900 = 2^2*5^2*7*17)
5[41]1 in base 46 = 1[41]5 in base 93 = 15[41] in base 109 (n=12467 = 7*13*137)
F91 in base 29 = 9F1 in base 37 = 19F in base 109 (n=12877 = 79*163)
F93 in base 29 = 9F3 in base 37 = 39F in base 64 (n=12879 = 3^5*53)
AP4 in base 35 = A4P in base 36 = 4AP in base 56 (n=13129 = 19*691)
BP2 in base 36 = B2P in base 37 = 2PB in base 81 (n=15158 = 2*11*13*53)
O6F in base 25 = FO6 in base 31 = 6FO in base 49 (n=15165 = 3^2*5*337)
FQ1 in base 31 = 1QF in base 111 = 1FQ in base 116 (n=15222 = 2*3*43*59)
B74 in base 37 = 7B4 in base 46 = 47B in base 61 (n=15322 = 2*47*163)

Can You Dij It? #1

Monday, 29th Feb, 2016 by Krilling for Company in Base Behavior, Binary numbers, Integer Sequences, Mathematics and tagged almost natural numbers, assembly language, base 10, base 9, binary, computers, decimal, digits, drugs, electronics, Integer Sequences, Language, machine code, math, mathemagic, mathemagick, mathematics, maths, natural languages, numbers, OEIS, Online Encyclopedia of Integer Sequences, reality, recreational math, recreational mathematics, recreational maths, water | 2 Comments

The most powerful drug in the world is water. The second most powerful is language. But everyone’s on them, so nobody realizes how powerful they are. Well, you could stop drinking water. Then you’d soon realize its hold on the body and the brain.

But you can’t stop using language. Try it. No, the best way to realize the power of language is to learn a new one. Each is a feast with different flavours. New alphabets are good too. The Devanagari alphabet is one of the strongest, but if you want it in refined form, try the phonetic alphabet. It will transform the way you see the world. That’s because it will make you conscious of what you’re already subconsciously aware of.

But “language” is a bigger category that it used to be. Nowadays we have computer languages too. Learning one is another way of transforming the way you see the world. And like natural languages – French, Georgian, Tagalog – they come in different flavours. Pascal is not like Basic is not like C is not like Prolog. But all of them seem to put you in touch with some deeper aspect of reality. Computer languages are like mathemagick: a way to give commands to something immaterial and alter the world by the application of will.

That feeling is at its strongest when you program with machine code, the raw instructions used by the electronics of a computer. At its most fundamental, machine code is simply a series of binary numbers controlling how a computer processes other binary numbers. You can memorize and use those code-numbers, but it’s easier to use something like assembly language, which makes machine-code friendlier for human beings. But it still looks very odd to the uninitiated:

setupnum:
xor ax,ax
xor bp,bp
mov cx,20
clearloop:
mov [di+bp],ax
add bp,2
loop clearloop
ret

That’s almost at the binary bedrock. And machine code is fast. If a fast higher-level language like C feels like flying a Messerschmitt 262, which was a jet-plane, machine-code feels like flying a Messerschmitt 163, which was a rocket-plane. A very fast and very dangerous rocket-plane.

I’m not good at programming languages, least of all machine code, but they are fun to use, quite apart from the way they make you feel as though you’re in touch with a deeper aspect of reality. They do that because the world is mathematics at its most fundamental level, I think, and computer languages are a form of mathematics.

Their mathematical nature is disguised in a lot of what they’re used for, but I like to use them for recreational mathematics. Machine-code is useful when you need a lot of power and speed. For example, look at these digits:

1, 2, 3, 4, 5, 6, 7, 8, 9, 1*, 0*, 1, 1, 1, 2, 1, 3, 1, 4, 1, 5, 1, 6, 1, 7, 1, 8, 1, 9, 2, 0, 2, 1, 2, 2, 2, 3, 2, 4, 2, 5, 2, 6, 2, 7, 2, 8, 2, 9, 3, 0, 3, 1, 3, 2, 3, 3, 3, 4, 3, 5, 3, 6*, 3*, 7, 3, 8, 3, 9, 4, 0, 4, 1, 4, 2, 4…

They’re what the Online Encyclopedia of Integer Sequences (OEIS) calls “the almost natural numbers” (sequence A007376) and you generate them by writing the standard integers – 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13… – and then separating each digit with a comma: 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 0, 1, 1, 1, 2, 1, 3… The commas give them some interesting twists. In a list of the standard integers, the 1st entry is 1, the 10th entry is 10, the 213rd entry is 213, the 987,009,381th entry is 987,009,381, and so on.

But that doesn’t work with the almost natural numbers. The 10th entry is 1, not 10, and the 11th entry is 0, not 11. But the 10th entry does begin the sequence (1, 0). I wondered whether that happened again. It does. The 63rd entry in the almost natural numbers begins the sequence (6, 3) – see the asterisks in the sequence above.

This happens again at the 3105th entry, which begins the sequence (3, 1, 0, 5). After that the gaps get bigger, which is where machine code comes in. An ordinary computer-language takes a long time to reach the 89,012,345,679th entry in the almost natural numbers. Machine code is much quicker, which is why I know that the 89,012,345,679th entry begins the sequence (8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 9):

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 63, 3105, 43108, 77781, 367573, 13859021, 77911127, 911360799, 35924813703, 74075186297, 89012345679…

And an ordinary computer-language might give you the impression that base 9 doesn’t have numbers like these (apart from the trivial 1, 2, 3, 4, 5, 6, 7, 8, 10…). But it does. 63 in base 10 is a low-hanging fruit: you could find it working by hand. In base 9, the fruit are much higher-hanging. But machine code plucks them with almost ridiculous ease:

1, 2, 3, 4, 5, 6, 7, 8, 10, 570086565, 655267526, 2615038272, 4581347024, 5307541865, 7273850617, 7801234568…

The Art Grows Onda

Thursday, 21st Jan, 2016 by Krilling for Company in Art, Fractals, Geometry, Mathematics, Rep-Tiles and tagged fractal, fractals, geometry, horned triangle, Ian Stewart, infinite geometry, infinite sum, Japanese art, Katsushi Hokusai, math, mathematics, maths, recreational math, recreational mathematics, recreational maths, tessellation, tessellations, The Great Wave off Kanagawa, triangle, Triangles, unicorn triangle, wave | Leave a comment

Anyone interested in recreational mathematics should seek out three compendiums by Ian Stewart: Professor Stewart’s Cabinet of Mathematical Curiosities (2008), Professor Stewart’s Hoard of Mathematical Treasures (2009) and Professor Stewart’s Casebook of Mathematical Mysteries (2014). They’re full of ideas and puzzles and are excellent introductions to the scope and subtlety of maths. I first came across Alexander’s Horned Sphere in one of them. I also came across this simpler shape that packs infinity into a finite area:

I call it a horned triangle or unicorn triangle and it reminds me of a wave curling over, like Katsushika Hokusai’s The Great Wave off Kanagawa (c. 1830) (“wave” is unda in Latin and onda in Spanish).

The Great Wave off Kanagawa by Katsushika Hokusai (1760–1849)

To construct the unicorn triangle, you take an equilateral triangle with sides of length 1 and erect a triangle with sides of length 0.5 on one of its corners. Then on the corresponding corner of the new triangle you erect a triangle with sides of length 0.25. And so on, for ever.

When you double the sides of a polygon, you quadruple the area: a 1×1 square has an area of 1, a 2×2 square has an area of 4. Accordingly, when you halve the sides of a polygon, you quarter the area: a 1×1 square has an area of 1, a 0.5 x 0.5 square has an area of 0.25 or 1/4. So if the original triangle of the unicorn triangle above has an area of 1 rather than sides of 1, the first triangle added has an area of 0.25 = 1/4, the next an area of 0.0625 = 1/16, and so on. The infinite sum is this:

1/4 + 1/16 + 1/256 + 1/1024 + 1/4096 + 1/16384…

Which equals 1/3. This becomes important when you see the use made of the shape in Stewart’s book. The unicorn triangle is a rep-tile, or a shape that can be divided into smaller copies of the same shape:

An equilateral triangle can be divided into four copies of itself, each 1/4 of the original area. If an equilateral triangle with an area of 4 is divided into three unicorn triangles, each unicorn has an area of 1 + 1/3 and 3 * (1 + 1/3) = 4.

Because it’s a rep-tile, a unicorn triangle is also a fractal, a shape that is self-similar at smaller and smaller scales. When one of the sub-unicorns is dropped, the fractals become more obvious:

$unicorn_fractal1$

$unicorn_fractal2$

$unicorn_fractal3$

Elsewhere other-posted:

• Rep-Tiles Revisited

Shareway to Seven

Thursday, 7th Jan, 2016 by Krilling for Company in Mathematics, Powers and tagged Arithmetic, integers, math, mathematical puzzles, mathematics, maths, powers, powers of 2, powers of 3, powers of 4, powers of 5, powers of two, Puzzles, recreational math, recreational mathematics, recreational maths | Leave a comment

An adaptation of an interesting distribution puzzle from Joseph Degrazia’s Math is Fun (1954):

After a successful year of plunder on the high seas, a pirate ship returns to its island base. The pirate chief, who enjoys practical jokes and has a mathematical bent, hands out heavy bags of gold coins to his seven lieutenants. But when the seven lieutenants open the bags, they discover that each of them has received a different number of coins.

They ask the captain why they don’t have equal shares. The pirate chief laughs and tells them to re-distribute the coins according to the following rule: “At each stage, the lieutenant with most coins must give each of his comrades as many coins as that comrade already possesses.”

The lieutenants follow the rule and each one in turn becomes the lieutenant with most coins. When the seventh distribution is over, all seven of them have 128 coins, the coins are fairly distributed, and the rule no longer applies.

The puzzle is this: How did the pirate captain originally allocate the coins to his lieutenants?

If you start at the beginning and work forward, you’ll have to solve a fiendishly complicated set of simultaneous equations. If you start at the end and work backwards, the puzzle will resolve itself almost like magic.

The puzzle is actually about powers of 2, because 128 = 2^7 and when each of six lieutenants receives as many coins as he already has, he doubles his number of coins. Accordingly, before the seventh and final distribution, six of the lieutenants must have had 64 coins and the seventh must have had 128 + 6 * 64 coins = 512 coins.

At the stage before that, five of the lieutenants must have had 32 coins (so that they will have 64 coins after the sixth distribution), one must have had 256 coins (so that he will have 512 coins after the sixth distribution), and one must have had 64 + 5 * 32 + 256 coins = 480 coins. And so on. This is what the solution looks like:

128, 128, 128, 128, 128, 128, 128
512, 64, 64, 64, 64, 64, 64
256, 480, 32, 32, 32, 32, 32
128, 240, 464, 16, 16, 16, 16
64, 120, 232, 456, 8, 8, 8
32, 60, 116, 228, 452, 4, 4
16, 30, 58, 114, 226, 450, 2
8, 15, 29, 57, 113, 225, 449

So the pirate captain must have originally allocated the coins like this: 8, 15, 29, 57, 113, 225, 449 (note how 8 * 2 – 1 = 15, 15 * 2 – 1 = 29, 29 * 2 – 1 = 57…).

The puzzle can be adapted to other powers. Suppose the rule runs like this: “At each stage, the lieutenant with most coins must give each of his comrades twice as many coins as that comrade already possesses.” If the pirate captain has six lieutenants, after each distribution each of five will have n + 2n = three times the number of coins that he previously possessed. The six lieutenants each end up with 729 coins = 3^6 coins and the solution looks like this:

13, 37, 109, 325, 973, 2917
39, 111, 327, 975, 2919, 3
117, 333, 981, 2925, 9, 9
351, 999, 2943, 27, 27, 27
1053, 2997, 81, 81, 81, 81
3159, 243, 243, 243, 243, 243
729, 729, 729, 729, 729, 729

For powers of 4, the rule runs like this: “At each stage, the lieutenant with most coins must give each of his comrades three times as many coins as that comrade already possesses.” With five lieutenants, each of them ends up with 1024 coins = 4^5 coins and the solution looks like this:

16, 61, 241, 961, 3841
64, 244, 964, 3844, 4
256, 976, 3856, 16, 16
1024, 3904, 64, 64, 64
4096, 256, 256, 256, 256
1024, 1024, 1024, 1024, 1024

For powers of 5, the rule runs like this: “At each stage, the lieutenant with most coins must give each of his comrades four times as many coins as that comrade already possesses.” With four lieutenants, each of them ends up with 625 coins = 5^4 coins and the solution looks like this:

17, 81, 401, 2001
85, 405, 2005, 5
425, 2025, 25, 25
2125, 125, 125, 125
625, 625, 625, 625

Shick Shtick

Friday, 18th Dec, 2015 by Krilling for Company in Logic, Mathematics, Puzzles and tagged brainteasers, Joseph Degrazia, logic, logic puzzle, logic puzzles, Math Is Fun, Puzzles, recreational math, recreational mathematics, recreational maths, six writers in a railway car | Leave a comment

Slightly adapted from Joseph Degrazia’s Math is Fun (1954):

Six Writers in a Railway Car

On their way to Chicago for a conference of authors and journalists, six writers meet in a railway club car. Three of them sit on one side facing the other three. Each of the six has his specialty. One writes short stories, one is a historian, another one writes humorous books, still another writes novels, the fifth is a playwright and the last a poet. Their names are Abbott, Blake, Clark, Duggan, Eccles and Farmer.* Each of them has brought one of his books and given it to one of his colleagues, so that each of the six is deep in a book which one of the other five has written.

Abbott reads a collection of short stories. Clark reads the book written by the colleague sitting just opposite him. Blake sits between the author of the short stories and the humorist. The short-story writer sits opposite the historian. Duggan reads a play. Blake is the brother-in-law of the novelist. Eccles sits next to the playwright. Abbott sits in a corner and is not interested in history. Duggan sits opposite the novelist. Eccles reads a humorous book. Farmer never reads poems.

These facts are sufficient to find each of the six authors’ specialties.

*In the original, the surnames were Blank, Bird, Grelly, George, Pinder and Winch.

Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral

მეფე (2) • მსოფლიოს (3) • მათემატიკა (5) •

Tag Archives: recreational maths