The French mathematician Siméon-Denis Poisson (1781-1840) once said: « La vie n’est bonne qu’à deux choses : à faire des mathématiques et à les professer. » — “Life is good only for two things: doing mathematics and teaching mathematics.” The German philosopher Nietzsche wouldn’t have agreed. He thought (inter alia) that we must learn to accept life as eternally recurring. Everything we do and experience will happen again and again for ever. Can you accept life like that? Then your life is good.

But neither Poisson or Nietzsche knew that Life, with a capital L, would take on a new meaning in the 20th century. It became a mathematical game played on a grid of squares with counters. You start by placing counters in some pattern, regular or random, on the grid, then you add or remove counters according to three simple rules applied to each square of the grid:

1. If an empty square has exactly three counters as neighbors, put a new counter on the square.
2. If a counter has two or three neighbors, leave it where it is.
3. If a counter has less than two or more than three neighbors, remove it from the grid.

And there is a meta-rule: apply all three rules simultaneously. That is, you check all the squares on the grid before you add or remove counters. With these three simple rules, patterns of great complexity and subtlety emerge, growing and dying in a way that reminded the inventor of the game, the English mathematician John Conway, of living organisms. That’s why he called the game Life.

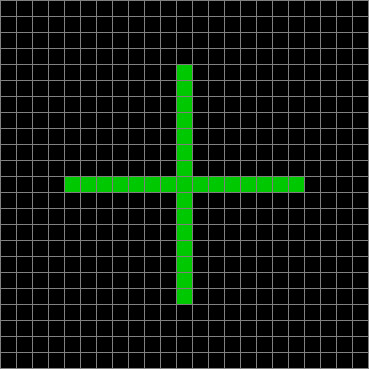
Let’s look at Life in action, with the seeding counters shown in green. Sometimes the seed will evolve and disappear, sometimes it will evolve into one or more fixed shapes, sometimes it will evolve into dynamic shapes that repeat again and again. Here’s an example of a seed that evolves and disappears:

Seeded with cross (arms 4+1+4) stage #1

Life stage #2

Life stage #3

Life stage #4

Life stage #5

Life stage #6

Life stage #7

Death at stage #8

Life from cross (animated)

The final stage represents death. Now here’s a cross that evolves towards dynamism:

Life seeded with cross (arms 3+1+3) stage #1

Life stage #2

Life stage #3

Life stage #4

Life stage #5

Life stage #6 (same as stage #4)

Life stage #7 (same as stage #5)

Life stage #8 (same as stage #4 again)

Life from cross (animated)

A line of three blocks swinging between horizontal and vertical is called a blinker:

Four blinkers

And here’s a larger cross that evolves towards stasis:

Life seeded with cross (arms 7+1+7) stage #1

Life stage #2

Life stage #3

Life stage #4

Life stage #5

Life stage #6

Life stage #7

Life stage #8

Life stage #9

Life stage #10

Life stage #11

Life stage #12

Life stage #13

Life stage #14

Life stage #15

Life stage #16

Life from cross (animated)

This diamond with sides of 24 blocks evolves towards even more dynamism:

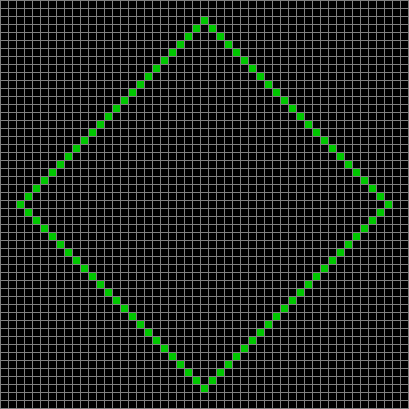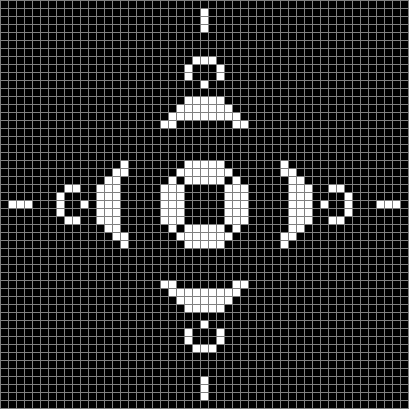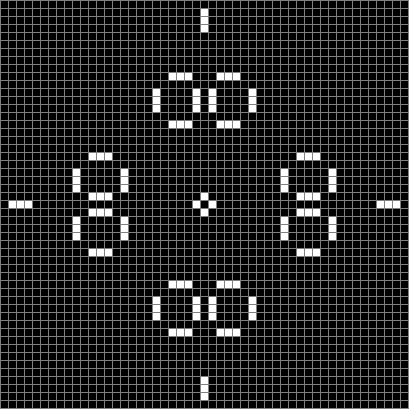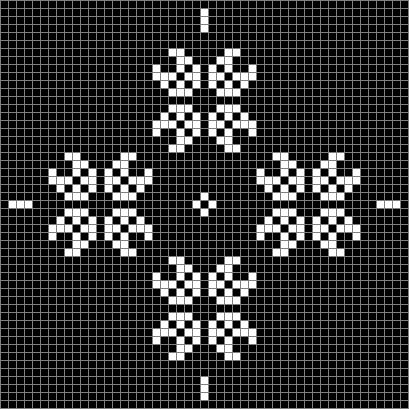
Life from 24-sided diamond (animated)

Looping Life from 24-sided diamond (animated)

The game of Life obviously has many variants. In the standard form, you’re checking all eight squares around the square whose fate is in question. If that square is (x,y), these are the eight other squares you check:

(x+1,y+1), (x+0,y+1), (x-1,y+1), (x-1,y+0), (x-1,y-1), (x+0,y-1), (x+1,y-1), (x+1,y+0)

Now trying checking only four squares around (x,y), the ones above and below and to the left and the right:

(x+1,y+1), (x-1,y+1), (x-1,y-1), (x+1,y-1)

And apply a different set of rules:

1. If a square has one or three neighbors, it stays alive or (if empty) comes to life
2. Otherwise the square remains or becomes empty.

With that check and those rules, the seed first disappears, then re-appears, for ever (note that the game is being played on a torus):

Evolution of spiral seed

Eternally recurring spiral

This happens with any seed, so you can use Life to bring Nietzsche’s eternal recurrence to life:

Evolution of LIFE

Eternally recurring LIFE